This topic covers work and change in kinetic/elastic potential energy.
This page will feature each question, as well as the options if the question is multiple choice (as noted by a "MC" tag just before the question number). Below each question will be the solution, in my own words. I attempt to be as precise and detailed as possible, but if you're still not getting something then just e-mail me and I will edit the explanation accordingly.
These are roughly ordered by their approximate difficulty (easiest to hardest), so I suggest not tackling a question unless you can solve everything above it. Please attempt the problems yourself before looking at the explanation.
A crate moves to the right on a horizontal surface as a woman pulls on it with a 10 N force. Rank the situations shown below according to the work done by the 10 N force, least to greatest. The displacement is the same for all cases.


A: In physics, "work" is defined by the formula W = Fs x cos(θ), where "F" is the force applied, "s" is the displacement of the object ("d" is also often used for this), and "θ" is the angle between the force and the displacement. In this case, the question explicitly states that the displacement is theoretically the same, so the only thing left to consider here is the force.
Technically, the forces are also all the same (10 N), but since the scenario proposed specifically relates to the block being pulled to the right, we have to focus solely on the X component of those forces.
Block 1 will clearly have the most work done, since all of the force is in the same direction as the motion. Force 2 is at an angle, so we know that will be smaller. The third image might be confusing, because the force is entirely in the vertical direction and there is no horizontal component at all. This is a little strange, in my opinion, as the question almost misleadingly implies that the displacement is always the same - but without any horizontal force, the block shouldn't be able to move at all. I believe what the question actually means is that we're to assume that the displacement is constant in theory for these blocks, even if the variables don't necessarily allow that to happen.
Either way, Block 3 won't be moving at all horizontally, so it will have the least amount of work done on it.
Technically, the forces are also all the same (10 N), but since the scenario proposed specifically relates to the block being pulled to the right, we have to focus solely on the X component of those forces.
Block 1 will clearly have the most work done, since all of the force is in the same direction as the motion. Force 2 is at an angle, so we know that will be smaller. The third image might be confusing, because the force is entirely in the vertical direction and there is no horizontal component at all. This is a little strange, in my opinion, as the question almost misleadingly implies that the displacement is always the same - but without any horizontal force, the block shouldn't be able to move at all. I believe what the question actually means is that we're to assume that the displacement is constant in theory for these blocks, even if the variables don't necessarily allow that to happen.
Either way, Block 3 won't be moving at all horizontally, so it will have the least amount of work done on it.
FINAL ANSWER: 3 < 2 < 1
(MC) An object moves in a circle at constant speed. The work done by the centripetal force is zero because:
Option 1: the average force for each revolution is zero
Option 2: the centripetal force is perpendicular to the velocity
Option 3: the displacement for each revolution is zero
Option 4: the magnitude of the acceleration is zero
Option 5: there is no friction
Option 1: the average force for each revolution is zero
Option 2: the centripetal force is perpendicular to the velocity
Option 3: the displacement for each revolution is zero
Option 4: the magnitude of the acceleration is zero
Option 5: there is no friction
A: I shouldn't need to explain why most of these options are obviously not it, but it's worth noting that Option 3 might seem pretty tempting; after all, the "d" for displacement in the formula for work does appear to indicate that an object travelling in a circle will ultimately have no work after one revolution. However, due to the vagueness of the question, we can't consider this the correct justification for why the work is always zero. After all, this explanation only applies whenever the total displacement is equal to a multiple of whatever the circumference of the circular path is. Besides, even if the question did specify this set of circumstances, there's a much better reason for why the work in this situation is always equal to zero.
Because most people simplify the work formula as just "force times distance", or "W = Fs", people often forget about the cos(θ) as well. Because the centripetal force/acceleration is always pointed inwards at a 90° angle to the velocity/tangent line at at given point, and since cos(90) is 0, this means that any centripetal acceleration is going to be zero.
Because most people simplify the work formula as just "force times distance", or "W = Fs", people often forget about the cos(θ) as well. Because the centripetal force/acceleration is always pointed inwards at a 90° angle to the velocity/tangent line at at given point, and since cos(90) is 0, this means that any centripetal acceleration is going to be zero.
FINAL ANSWER: Option 2 (the centripetal force is perpendicular to the velocity)
(MC) A man pulls a sled along a rough horizontal surface by applying a constant force F at an angle θ above the horizontal. In pulling the sled a horizontal distance d, the work done by the man is:
Option 1: Fd/cos η
Option 2: Fd
Option 3: Fd cos η
Option 4: Fd/sin η
Option 5: Fd sin η
Option 1: Fd/cos η
Option 2: Fd
Option 3: Fd cos η
Option 4: Fd/sin η
Option 5: Fd sin η
A: A very simple question, really. We used the "W = Fscos(θ)" in both of the above questions. It's just the same thing here, asked even more simply and without any caveats or twists on the question. So...
FINAL ANSWER: Option 3: Fd cos η
(MC) Which of the following bodies has the largest kinetic energy?
1. Mass 3M and speed 2V
2. Mass 2M and speed 3V
3. All four of these have the same kinetic energy
4. Mass 3M and speed V
5. Mass M and speed 4V
1. Mass 3M and speed 2V
2. Mass 2M and speed 3V
3. All four of these have the same kinetic energy
4. Mass 3M and speed V
5. Mass M and speed 4V
A: Recall the kinetic energy formula:
KE = 1/2 mv2
Now, although we're not given any values to plug into this formula and output an exact answer, we can take the coefficients we're given in the options and see what this formula does to them. For instance option 1 tells us that there's a 3M and 2V. Let's place this into our KE formula.
KE = 1/2 3M(2V)2
Now, let's rewrite this a bit to get a better idea of how exactly these coefficients are impacting the amount of kinetic energy.
KE = 1/2 3M 4(V2) = 12 (1/2 MV2)
As you can see, I've written the "original" KE formula along with a single coefficient on the outside. 12. The idea here is that we'll want to keep doing this for our options to see which result yields the largest "outside" number. Obviously, whatever the number is for V will make that number increase the fastest due to the fact that velocity is squared in the kinetic energy formula. Because of that, the 4V seems like a pretty tempting answer. Be careful though - in that one there's no number at all in front of the M, so that could have a negative impact. Let's try both of our options that have higher values for V and see how the math works out. The answer then becomes pretty clear:
KE = 1/2 M(4V)2 = 1/2 M 16(V2) = 16(1/2MV2)
KE = 1/2 2M(3V)2 = 1/2 2M 9(V2) = 18(1/2MV2)
KE = 1/2 mv2
Now, although we're not given any values to plug into this formula and output an exact answer, we can take the coefficients we're given in the options and see what this formula does to them. For instance option 1 tells us that there's a 3M and 2V. Let's place this into our KE formula.
KE = 1/2 3M(2V)2
Now, let's rewrite this a bit to get a better idea of how exactly these coefficients are impacting the amount of kinetic energy.
KE = 1/2 3M 4(V2) = 12 (1/2 MV2)
As you can see, I've written the "original" KE formula along with a single coefficient on the outside. 12. The idea here is that we'll want to keep doing this for our options to see which result yields the largest "outside" number. Obviously, whatever the number is for V will make that number increase the fastest due to the fact that velocity is squared in the kinetic energy formula. Because of that, the 4V seems like a pretty tempting answer. Be careful though - in that one there's no number at all in front of the M, so that could have a negative impact. Let's try both of our options that have higher values for V and see how the math works out. The answer then becomes pretty clear:
KE = 1/2 M(4V)2 = 1/2 M 16(V2) = 16(1/2MV2)
KE = 1/2 2M(3V)2 = 1/2 2M 9(V2) = 18(1/2MV2)
FINAL ANSWER: Option 2 (Mass 2M and speed 3V)
(MC) The amount of work required to stop a moving object is equal to the:
1. mass of the object times its velocity
2. velocity of the object
3. square of the velocity of the object
4. mass of the object times its acceleration
5. kinetic energy of the object
1. mass of the object times its velocity
2. velocity of the object
3. square of the velocity of the object
4. mass of the object times its acceleration
5. kinetic energy of the object
A: I mean. Think about what energy is: It's generally defined by scientists as "the ability to do work". The concepts of work and energy are directly related to one another; they even typically use the same units (joules). If you want to stop an object from moving with a certain amount of work, it's gonna have to be equal (and negative) to the number of joules with which the object is currently moving.
FINAL ANSWER: Option 5 (kinetic energy of the object)
(MC) A Boston Red Sox baseball player catches a ball of mass m that is moving toward him with speed v. While bringing the ball to rest, his hand moves back a distance d. Assuming constant deceleration, the horizontal force exerted on the ball by his hand is:
1. mv2/(2d)
2. 2mv/d
3. mv2/d
4. mvd
5. mv/d
1. mv2/(2d)
2. 2mv/d
3. mv2/d
4. mvd
5. mv/d
A: The ball is described as going from a known velocity (v) to rest over the known distance (d) of the hand's movement. This means that the hand is doing work on the ball over this distance.
Naturally, we'd want to use the work formula (W = Fd) on this, but since the work variable "W" isn't included in any of the multiple choice options, we'll have to find an answer in terms of m, v, and d. As discussed in the previous problem, the work done to bring an object to rest should be equal to that object's initial kinetic energy, so let's substitute "W" in our formula with the kinetic energy formula and solve for F:
1/2 mv2 = Fd -> mv2/(2d) = F (the "1/2" is turned into simply a 2 in the denominator for further simplification)
Naturally, we'd want to use the work formula (W = Fd) on this, but since the work variable "W" isn't included in any of the multiple choice options, we'll have to find an answer in terms of m, v, and d. As discussed in the previous problem, the work done to bring an object to rest should be equal to that object's initial kinetic energy, so let's substitute "W" in our formula with the kinetic energy formula and solve for F:
1/2 mv2 = Fd -> mv2/(2d) = F (the "1/2" is turned into simply a 2 in the denominator for further simplification)
FINAL ANSWER: Option 1 (mv2/(2d))
(MC) In raising an object to a given height by means of an inclined plane, as compared with raising the object vertically, there is a reduction in:
1. work required
2. friction
3. distance pushed
4. value of the acceleration due to gravity
5. force required
1. work required
2. friction
3. distance pushed
4. value of the acceleration due to gravity
5. force required
A: The common wrong answer here would probably be, if I had to guess, work required. Someone might assume that pushing the object along an incline will decrease the work in the sense that it becomes easier to move, but this is incorrect. In fact, work won't change at all in this scenario; Since we're still moving the block the same vertical distance upwards in both cases, the W = Fd formula isn't changing in either case, and both systems are being converted to the same amount of potential energy (assuming we're using the same exact object in both scenarios).
However, something important is being altered by this longer travel distance. Although the upwards component of F isn't changing at all, because the total travel distance is longer and because there's an angle, the force's total magnitude has become smaller (it's now either Fcos(θ) or Fsin(θ), depending on how you prefer to look at the problem). The force needed to move the block has gone down.
However, something important is being altered by this longer travel distance. Although the upwards component of F isn't changing at all, because the total travel distance is longer and because there's an angle, the force's total magnitude has become smaller (it's now either Fcos(θ) or Fsin(θ), depending on how you prefer to look at the problem). The force needed to move the block has gone down.
FINAL ANSWER: Option 5 (force required)
(MC) A woman lifts a barbell 2.0 m in 5.0 s. If she lifts it the same distance in 10 s, the work done by her is:
1. the same
2. four times as great
3. half as great
4. one-fourth as great
5. two times as great
1. the same
2. four times as great
3. half as great
4. one-fourth as great
5. two times as great
A: Don't forget what work is. Just taking a quick look at the formula for work will remind you that the amount of work done on a system is based on the distance and the force applied, neither of which are being altered here in this scenario.
FINAL ANSWER: Option 1 (the same)
(MC) A particle starts from rest and is acted on by a net force that does work at a rate that is proportional to the time t. The speed of the particle is proportional to:
1.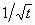
2. t
3.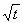
4. t2
5. 1/t
1.
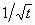
2. t
3.
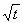
4. t2
5. 1/t
A: Proportionality questions always seem to confuse people, which is understandable because they can get somewhat abstract at times. This one should be simple enough though; we're looking for a relationship between time and the velocity of a moving particle.
We're talking about work in the context of a particle accelerating from rest, so let's use the KE formula in our analysis. After all, the KE formula has the velocity variable v, so we'll want to use that. (As a side note, I wouldn't use the Fd formula because you would have to make several substitutions in a row that would result in too many assumptions about the system and the constancy of its acceleration - I tried using it to see what the answer would be and sure enough, it was wrong. The KE formula is more universal for this sort of question and is much easier to use anyway.)
Anyway, since the details we're given in the problem is that the work is "proportional" to the time t without many other details, let's just arbitrarily set KE equal to t and isolate v:
1/2 mv2 = t -> v = sqrt(2t/m)
As you can see, if we ignore the irrelevant variables and only focus on v and t (the other variables don't affect this relationship at all), then v is correlated with the square root of t.
We're talking about work in the context of a particle accelerating from rest, so let's use the KE formula in our analysis. After all, the KE formula has the velocity variable v, so we'll want to use that. (As a side note, I wouldn't use the Fd formula because you would have to make several substitutions in a row that would result in too many assumptions about the system and the constancy of its acceleration - I tried using it to see what the answer would be and sure enough, it was wrong. The KE formula is more universal for this sort of question and is much easier to use anyway.)
Anyway, since the details we're given in the problem is that the work is "proportional" to the time t without many other details, let's just arbitrarily set KE equal to t and isolate v:
1/2 mv2 = t -> v = sqrt(2t/m)
As you can see, if we ignore the irrelevant variables and only focus on v and t (the other variables don't affect this relationship at all), then v is correlated with the square root of t.
FINAL ANSWER: Option 3 (Square root of t)
If a Saturn V rocket with an Apollo spacecraft attached has a combined mass of 2.9 ✕ 105 kg and reached a speed of 11.2 km/s, how much kinetic energy would it then have?
A: We're only looking for kinetic energy here, so let's just plug these values into our kinetic energy formula. And be sure to multiply the velocity by 1000 to convert it from km/s to m/s:
1/2 mv2 = 1/2 (2.9 x 105 kg)[(11.2km/s)(1000m)/(1km)]2 = 18188800000000 joules, or 1.82E13 J.
1/2 mv2 = 1/2 (2.9 x 105 kg)[(11.2km/s)(1000m)/(1km)]2 = 18188800000000 joules, or 1.82E13 J.
FINAL ANSWER: 1.82E13 J
A proton (mass m = 1.67 ✕ 10-27 kg) is being accelerated along a straight line at 3.1 ✕ 1015 m/s2 in a machine. The proton has an initial speed of 2.4 ✕ 107 m/s and travels 2.7 cm.
(a) What is its speed? (Give your answer to at least four significant figures.)
(b) What is the increase in its kinetic energy?
(a) What is its speed? (Give your answer to at least four significant figures.)
(b) What is the increase in its kinetic energy?
A: (a) Let's use our kinematics equations for this. Using the v2 formula:
v = sqrt(v02 + 2ad) = sqrt[(2.4 x 107 m/s)2 + 2(3.1 x 1015 m/s2)([2.7 cm][0.01 m])] = 2.72654E7 m/s
(b) To find the change in kinetic energy, we'll just have to subtract the initial kinetic energy from the final KE, using the final velocity we calculated in the last part.
ΔKE = KEf - KEi = 1/2 mvf2 - 1/2 mvi2 = 1/2 (1.67 x 10-27 kg)(2.72654E7 m/s)2 - 1/2 (1.67 x 10-27 kg)(2.4E7 m/s)2 = 1.39781E-13 J
v = sqrt(v02 + 2ad) = sqrt[(2.4 x 107 m/s)2 + 2(3.1 x 1015 m/s2)([2.7 cm][0.01 m])] = 2.72654E7 m/s
(b) To find the change in kinetic energy, we'll just have to subtract the initial kinetic energy from the final KE, using the final velocity we calculated in the last part.
ΔKE = KEf - KEi = 1/2 mvf2 - 1/2 mvi2 = 1/2 (1.67 x 10-27 kg)(2.72654E7 m/s)2 - 1/2 (1.67 x 10-27 kg)(2.4E7 m/s)2 = 1.39781E-13 J
FINAL ANSWER: (a) 2.72654E7 m/s
(b) 1.39781E-13 J
(b) 1.39781E-13 J
A father racing his son has three-fifths the kinetic energy of the son, who has three-fifths the mass of the father. The father speeds up by 1.0 m/s and then has the same kinetic energy as the son.
(a) What is the original speed of the father?
(b) What is the original speed of the son?
(a) What is the original speed of the father?
(b) What is the original speed of the son?
A: A very tricky problem. (a) Because all of our variables are defined in terms of other versions of the same variable, let's first try and rewrite the problem so that we'll get to use as many of the same consistent variables as we can. Let Ks be the son's kinetic energy, Ki be the father's initial kinetic energy, and Kf be the father's final kinetic energy. Let's get a formula in terms of just the father's kinetic energy:
Ki = 3/5 Ks, and Kf = Ks (as given by the problem). Therefore, Ki = 3/5 Kf. Now we have an equation in terms of just the father's variables. Let's expand this a bit:
1/2 mvi2 = 3/5 [1/2 m(vi + 1.0 m/s)2]. Simplify this a bit further and we get:
2/5vi2 - 6/5vi - 3/5 = 0. Now, simply use the quadratic formula on this and take the positive answer and we get approximately 3.43649 m/s.
(b) Generally the same process as part (a), but it's slightly easier now because we've already solved for a variable that will help us. Setting our K values to include the son's variables and expanding them again:
Ki = 3/5Ks --> 1/2 mvi2 = 3/5 (1/2 x 3/5 mv22). Simplify, sub in our answer in (a) for vi and solve for vs. The answer should be 5.72748.
Ki = 3/5 Ks, and Kf = Ks (as given by the problem). Therefore, Ki = 3/5 Kf. Now we have an equation in terms of just the father's variables. Let's expand this a bit:
1/2 mvi2 = 3/5 [1/2 m(vi + 1.0 m/s)2]. Simplify this a bit further and we get:
2/5vi2 - 6/5vi - 3/5 = 0. Now, simply use the quadratic formula on this and take the positive answer and we get approximately 3.43649 m/s.
(b) Generally the same process as part (a), but it's slightly easier now because we've already solved for a variable that will help us. Setting our K values to include the son's variables and expanding them again:
Ki = 3/5Ks --> 1/2 mvi2 = 3/5 (1/2 x 3/5 mv22). Simplify, sub in our answer in (a) for vi and solve for vs. The answer should be 5.72748.
FINAL ANSWERS: (a) 3.43649 m/s
(b) 5.72748 m/s
(b) 5.72748 m/s
A box of a 7.0 kg, full of dangerous chemical powder, is being pushed by a 5.0 N force that makes it move in an xy plane. The box has an initial velocity of 5.0 m/s in the positive x direction and some time later has a velocity of 7.0 m/s in the positive y direction. How much work is done on the box by the force during this time?
A: We're looking for the work done on a single moving object, so let's simply take its initial and final velocities and put that into our KE formulas to find the difference. In truth, the xy-coordinates and the fact that its motion switches axes doesn't really matter, since energy is a scalar and isn't affected by the direction of the motion.
ΔKE = 1/2 mvf2 - 1/2 mvi2 = 1/2 (7.0kg)(7.0m/s)2 - 1/2 (7.0kg)(5.0m/s)2 = 84 J
ΔKE = 1/2 mvf2 - 1/2 mvi2 = 1/2 (7.0kg)(7.0m/s)2 - 1/2 (7.0kg)(5.0m/s)2 = 84 J
FINAL ANSWER: 84 J
A startled mouse slides over a patch of ice (frictionless surface) and across an xy coordinate system from the origin to a point with xy coordinates (3.0 m, 3.8 m) while a mischievous cat pushes on it. The cat uses a 2.1 N force on the mouse and is pushing at a counterclockwise angle of 100° from the positive direction of the x axis. How much work is done by the cat on the panicked mouse during the displacement?
A: We're given force and distance, so we can once again use our W = Fd equation for this. First, write out the force components with their respective unit vectors:
F = (2.1cos100N)i + (2.1sin100N)j
Let's multiply these by the displacement vectors we're already given to calculate work.
W = [(3.0m)i + (3.8m)j] x [(2.1cos100N)i + (2.1sin100N)j]
Now do the math, but keep in mind that you can only multiple vectors that have like directions:
W = (3.0m x 2.1cos100N) + (3.8m x 2.1sin100N) = 6.76478 J
F = (2.1cos100N)i + (2.1sin100N)j
Let's multiply these by the displacement vectors we're already given to calculate work.
W = [(3.0m)i + (3.8m)j] x [(2.1cos100N)i + (2.1sin100N)j]
Now do the math, but keep in mind that you can only multiple vectors that have like directions:
W = (3.0m x 2.1cos100N) + (3.8m x 2.1sin100N) = 6.76478 J
FINAL ANSWER: 6.76478 J
A floating ice block is pushed through a displacement d = (23 m)i - (13 m)j along a straight embankment by rushing water, which exerts a force F = (178 N)i- (117 N)j on the block. How much work does the force do on the block during the displacement?
A: Similarly to the above problem, just multiply the components by their corresponding counterparts and add them together. I say "add" instead of "subtract" because work is a scalar - if you try to subtract the values just because of the minus sign in the j values then it will screw up your answer.
W = Fd = [(178N)i - (117N)j] x [(23m)i - (13m)j] = (178N)i x (23m)i + (117N)i x (117N)j = 5615 J
W = Fd = [(178N)i - (117N)j] x [(23m)i - (13m)j] = (178N)i x (23m)i + (117N)i x (117N)j = 5615 J
FINAL ANSWER: 5615 J
An 9.6 kg object is moving in the positive direction of an x axis. When it passes through x = 0, a constant force directed along the axis begins to act on it. The figure below gives its kinetic energy K versus position x as it moves from x = 0 to x= 5.0 m; K0 = 24.5 J. The force continues to act. What is v when the object moves back through x = -3.0 m?
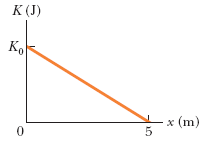

A: We could probably use the graph to calculate work as the area under the curve and go from there, but there's a nifty little shortcut we could take. Although K0 in this context is meant to represent "energy" rather than work, we already know it's going to be equal to work - as discussed in some problems above, the work needed to get it to slow down to rest will have to be equal to the amount of kinetic energy the object initially has. Therefore, let's set K0 equal to work (Fd), and expand the formula to solve for the acceleration:
K0 = Fd = mad -> a = K0/(md) = 24.5J/[(9.6kg)(5.0m)] = 0.510417m/s2
Now plug this into the kinematics formulas to solve for the velocity at the position of -3m. The acceleration is beginning at +5m, so the total displacement to use in the formula will be 5.0m - (-3.0m) = 8.0m.
v = sqrt[(2)(.510417m/s2)(8.0m)] = 2.85774 m/s
K0 = Fd = mad -> a = K0/(md) = 24.5J/[(9.6kg)(5.0m)] = 0.510417m/s2
Now plug this into the kinematics formulas to solve for the velocity at the position of -3m. The acceleration is beginning at +5m, so the total displacement to use in the formula will be 5.0m - (-3.0m) = 8.0m.
v = sqrt[(2)(.510417m/s2)(8.0m)] = 2.85774 m/s
FINAL ANSWER: 2.85774 m/s
A can of bolts and nuts is pushed 2.00 m along an x axis by a broom along the greasy (frictionless) floor of a car repair shop in a version of shuffleboard. The figure below gives the work W done on the can by the constant horizontal force from the broom, versus the can's position x.
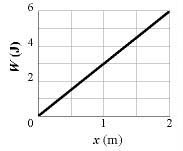
(a) What is the magnitude of that force?
(b) If the can had an initial kinetic energy of 2.60 J, moving in the positive direction of the x axis, what is its kinetic energy at the end of the 2.00 m displacement?

(a) What is the magnitude of that force?
(b) If the can had an initial kinetic energy of 2.60 J, moving in the positive direction of the x axis, what is its kinetic energy at the end of the 2.00 m displacement?
A: This question is fairly easy. In fact, you almost don't even need to read the problem at all - the graph tells us everything we need to know to answer the two questions.
(a) We already established that the area under the curve of a Force-displacement graph is equal to the amount of work done. It naturally follows, of course, that the slope of a Work-displacement graph would be equal to the force applied. 6J/2m = 3N
(b) Once again, work applied to an object is equal to its change in kinetic energy, so let's just add the amount of work we're doing to the object's initial kinetic energy. 2.60J + 6.00 J = 8.60J
(a) We already established that the area under the curve of a Force-displacement graph is equal to the amount of work done. It naturally follows, of course, that the slope of a Work-displacement graph would be equal to the force applied. 6J/2m = 3N
(b) Once again, work applied to an object is equal to its change in kinetic energy, so let's just add the amount of work we're doing to the object's initial kinetic energy. 2.60J + 6.00 J = 8.60J
FINAL ANSWER: (a) 3N
(b) 8.60J
(b) 8.60J
In the figure below, a block of ice slides down a frictionless ramp at angle θ = 50°, while an ice worker pulls up the ramp (via a rope) with a force of magnitude Fr = 40 N. As the block slides through distance d = 0.40 m along the ramp, its kinetic energy increases by 75 J. How much greater would its kinetic energy have been if the rope had not been attached to the block?
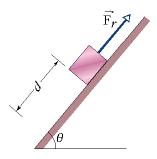

A: This problem looks daunting, but is actually very simple. We're only looking for a difference in kinetic energy, so let's just figure out exactly how much work the rope force Fr is doing on the block over the motion described. The block is sliding down the ramp over a distance of 0.40m with a force from the rope of 40N. Plug these variables into the work formula and we get W = Fd = (40N)(0.40m) = 16J. This is how much negative work that the rope is doing on the block, so without the force of the rope, this is how much more kinetic energy the block would have.
FINAL ANSWER: 16J
In the figure below, we must apply a force of magnitude 87 N to hold the block stationary at x = -2.0 cm. From that position we then slowly move the block so that our force does +3.4 J of work on the spring-block system; the block is then again stationary. What is the block's position (x)? (There are two answers.)
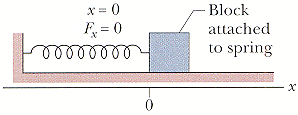

A: First, let's find the spring constant with Hooke's Law. This is easy since we're given a force of 87N and a compressed distance of 2.0cm (0.02m).
F = -kx -> k = F/-x = 87N/-0.02m = 4350N/m
Now, we can use our force/energy equations. The typical term used for finding work in a spring force is 1/2kx2, but since our starting position for the work's application isn't at the spring's rest position, we'll have to use the slightly more complicated version of the formula:
Ws = 1/2kxi2 - 1/2kxf2 ; Where xi is the position of the object when we begin applying our work, and xf is the object's final position (note that both positions are relative to a coordinate system in which "x = 0" represents the location of the spring's resting position without any force being applied). Solve for xf by subbing in all the other known values and using algebra, and we get 0.044308m, in either the positive or negative direction. The positive value is going to be more accurate for what this particular problem is asking, but for some reason this question wants us to give both the positive and negative values. Okay...? Also, we have to answer in units of centimeters, so multiply both of the answers by 100 as well.
F = -kx -> k = F/-x = 87N/-0.02m = 4350N/m
Now, we can use our force/energy equations. The typical term used for finding work in a spring force is 1/2kx2, but since our starting position for the work's application isn't at the spring's rest position, we'll have to use the slightly more complicated version of the formula:
Ws = 1/2kxi2 - 1/2kxf2 ; Where xi is the position of the object when we begin applying our work, and xf is the object's final position (note that both positions are relative to a coordinate system in which "x = 0" represents the location of the spring's resting position without any force being applied). Solve for xf by subbing in all the other known values and using algebra, and we get 0.044308m, in either the positive or negative direction. The positive value is going to be more accurate for what this particular problem is asking, but for some reason this question wants us to give both the positive and negative values. Okay...? Also, we have to answer in units of centimeters, so multiply both of the answers by 100 as well.
A: -4.43082cm (smaller value), 4.43082cm (larger value)
The only force acting on a 1.7 kg body as it moves along the positive x axis has an x component Fx = - 6x N, where x is in meters. The velocity of the body at x = 3.0 m is 8.0 m/s.
(a) What is the velocity of the body at x = 4.0 m?
(b) At what positive value of x will the body have a velocity of 5.0 m/s?
(a) What is the velocity of the body at x = 4.0 m?
(b) At what positive value of x will the body have a velocity of 5.0 m/s?
A: Don't bother with this one unless you know calculus. In particular, this question involves (relatively basic) integration, which I'm not going to explain here.
(a) Since our force value is given in terms of x, this means that the force is not constant in this problem! Oh no! This means that none of our common algebraic formulas will work here. However, we ARE given the object's velocity at x = 3.0m, and we're looking for the velocity at x = 4.0m, so this can help us. We'll want to find the work applied to the object over this integral. However, because F is written in terms of x, in order to find work we'll have to do some integration. Let's take the integral of the force function F = -6x, and use the fundamental theorem of calculus to find the amount of work over the interval from the x-positions 3.0m to 4.0m. This gives us -21 joules.
This value represents the applied work, or the change in kinetic energy. Let's use our KE formulas to find the final velocity.
W = ΔKE = 1/2m(vf2 - vi2) -> Solve this for vf and plug in our other values (using 8m/s for initial velocity) to get 6.2685m/s for final velocity.
(b) In this part, we're looking for a position based on a projected velocity. The method is overall the same, but our equation will be a little more complicated because we don't have a value for W to use (we're searching for a displacement, so we don't have any way of knowing yet how much work was done in this scenario). The integral you should have calculated in the previous part would have looked like this:
Wx = -3(xf2 - xi2)
This equation is equal to the work applied. Set it equal to the ΔKE formula like we did for the previous part:
-3(xf2 - xi2) = 1/2m(vf2 - vi2) -> Solve for xf to get an answer of 4.47772m.
(a) Since our force value is given in terms of x, this means that the force is not constant in this problem! Oh no! This means that none of our common algebraic formulas will work here. However, we ARE given the object's velocity at x = 3.0m, and we're looking for the velocity at x = 4.0m, so this can help us. We'll want to find the work applied to the object over this integral. However, because F is written in terms of x, in order to find work we'll have to do some integration. Let's take the integral of the force function F = -6x, and use the fundamental theorem of calculus to find the amount of work over the interval from the x-positions 3.0m to 4.0m. This gives us -21 joules.
This value represents the applied work, or the change in kinetic energy. Let's use our KE formulas to find the final velocity.
W = ΔKE = 1/2m(vf2 - vi2) -> Solve this for vf and plug in our other values (using 8m/s for initial velocity) to get 6.2685m/s for final velocity.
(b) In this part, we're looking for a position based on a projected velocity. The method is overall the same, but our equation will be a little more complicated because we don't have a value for W to use (we're searching for a displacement, so we don't have any way of knowing yet how much work was done in this scenario). The integral you should have calculated in the previous part would have looked like this:
Wx = -3(xf2 - xi2)
This equation is equal to the work applied. Set it equal to the ΔKE formula like we did for the previous part:
-3(xf2 - xi2) = 1/2m(vf2 - vi2) -> Solve for xf to get an answer of 4.47772m.
FINAL ANSWERS: (a) 6.2685m/s
(b) 4.47772m
(b) 4.47772m
In Figure (a), a block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (spring constant k) whose other end is fixed. The block is initially at rest at the position where the spring is unstretched (x = 0) when a constant horizontal force vector F in the positive direction of the x axis is applied to it. A plot of the resulting kinetic energy of the block versus its position x is shown in Figure (b). The scale of the figure's vertical axis is set by Ks = 4.4 J and the scale of the figure's horizontal axis is set by xmax = 4.4 m.
Fig. (a): Fig. (b):
Fig. (b): 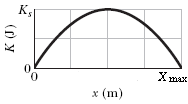
(a) What is the magnitude of vector F?
(b) What is the value of k?
Fig. (a):
 Fig. (b):
Fig. (b): 
(a) What is the magnitude of vector F?
(b) What is the value of k?
A: (a) The graph clues us into the relationship between the kinetic energy, so let's write a formula for kinetic energy K of the block as a function of position x. Taking the origin at the relaxed position, creating an equation with the works done by the spring and the applied force (-(1/2)kx2 and Fx respectively), we get:
ΔK = W ⇒ K = -(1/2)kx2 + Fx
Now, let's plug in the x-position values 2.2 (the point with the max highest kinetic energy) and 4.4 (the point at the end, with zero kinetic energy but the highest x-value) into this equation to get a system of equations for our results:
4.4J = -(1/2)k(2.2m)2 + F(2.2m) ⇒ 4.4J = -2.42k + 2.2F
0 = -(1/2)k(4.4m)2 + F(4.4m) ⇒ 0 = -9.68k + 4.4F
The second equation is equal to zero, so we can easily set it equal to a particular variable and plug it into the other equation. The problem just becomes basic algebra at this point. The results you get are F = 4N and k = 1.81818N/m.
ΔK = W ⇒ K = -(1/2)kx2 + Fx
Now, let's plug in the x-position values 2.2 (the point with the max highest kinetic energy) and 4.4 (the point at the end, with zero kinetic energy but the highest x-value) into this equation to get a system of equations for our results:
4.4J = -(1/2)k(2.2m)2 + F(2.2m) ⇒ 4.4J = -2.42k + 2.2F
0 = -(1/2)k(4.4m)2 + F(4.4m) ⇒ 0 = -9.68k + 4.4F
The second equation is equal to zero, so we can easily set it equal to a particular variable and plug it into the other equation. The problem just becomes basic algebra at this point. The results you get are F = 4N and k = 1.81818N/m.
FINAL ANSWERS: (a) 4N
(b) 1.81818N/m
(b) 1.81818N/m
A 4.0 kg block moves in a straight line on a horizontal frictionless surface under the influence of a force that varies with position as shown below. How much work is done by the force as the block moves from the origin to x = 8.0 m?
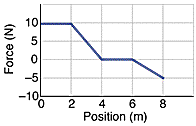

A: As this is a force-position graph, you simply have to calculate the area under the curve. Pay attention to where the x = 0 line is. The positive work is 30J, and the negative work is 5J. 30J - 5J = 25J.
FINAL ANSWER: 25J
A 1.3 kg hockey puck is initially at rest on the ice when a hockey player pushes on it with his stick, with a perfectly horizontal force in the positive direction of an x axis. The resulting force from the hockey stick is given by F(x) = (2.5 - x2)i N, where x is in meters and the initial position of the puck is x = 0.
(a) What is the kinetic energy of the puck as it passes through the blue line at x = 2.0 m?
(b) What is the maximum kinetic energy of the puck between x = 0 and x = 2.0 m?
(a) What is the kinetic energy of the puck as it passes through the blue line at x = 2.0 m?
(b) What is the maximum kinetic energy of the puck between x = 0 and x = 2.0 m?
A: (a) We're given force as a function of position just like in one of the last questions, so we'll use the fact that work is equal to the integral of force with respect to position. The definite integral of 2.5 - x2 over the interval of 0 to 2.0m is 2.33333J.
(b) To find where the KE will be the highest, let's first set the force function equal to zero to find out where the work function would have reached its peak:
2.5 - x2 = 0 ⇒ x = sqrt(2.5)
Now let's once again use the Fundamental Theorem of Calculus (FTC) on the integral of the same force function, except using the square root of 2.5 as the upper bound instead. This gets us 2.64J.
(b) To find where the KE will be the highest, let's first set the force function equal to zero to find out where the work function would have reached its peak:
2.5 - x2 = 0 ⇒ x = sqrt(2.5)
Now let's once again use the Fundamental Theorem of Calculus (FTC) on the integral of the same force function, except using the square root of 2.5 as the upper bound instead. This gets us 2.64J.
FINAL ANSWERS: (a) 2.33333J
(b) 2.64J
(b) 2.64J
A 100 kg block is pulled at a constant speed of 6.0 m/s across a horizontal floor by an applied force of 133 N directed 37° above the horizontal. What is the rate at which the force does work on the block?
A: We're looking for rate of change, AKA power (work over time). Let's set up the power formula and break it down to a form with variables we can use:
Pavg = W/Δt = (F dx cosθ)/(dt) = Fvcosθ = (133N)(6m/s)(cos(37)) = 637.311 watts.
Pavg = W/Δt = (F dx cosθ)/(dt) = Fvcosθ = (133N)(6m/s)(cos(37)) = 637.311 watts.
FINAL ANSWER: 637.311W
In an Amazon distribution center, a fancy machine carries a 3.0 kg package for Dr. Padalino. The package started from an initial position of di = (0.50 m)i + (0.75 m)j + (0.20 m)k at t = 0 to a final position of df = (7.00 m)i + (11.0 m)j + (7.50 m)k at t = 15 s. The constant force applied by the machine to move the package is F = (2.00 N)i + (4.00 N)j + (6.00 N)k.
(a) For that displacement, find the work done on the package by the machine's force.
(b) Also, find the power of the machine's force on the package.
(a) For that displacement, find the work done on the package by the machine's force.
(b) Also, find the power of the machine's force on the package.
A: (a) First let's find the displacement between the starting and ending positions.
df - di = (7.00 m)i + (11.0 m)j + (7.50 m)k - [(0.50 m)i + (0.75 m)j + (0.20 m)k] = (6.50m)i + (10.25m)j + (7.30m)k
Multiply this by the force vectors to calculate work.
W = Fd = [(2.00 N)i + (4.00 N)j + (6.00 N)k] × [(6.50m)i + (10.25m)j + (7.30m)k] = (13J)i + (41J)j + (43.8J)k = 97.8J
(b) To find the power of a force, divide work by time (the time we're given in the problem is 15 seconds).
P = W/Δt = 97.8J/15s = 6.52W
df - di = (7.00 m)i + (11.0 m)j + (7.50 m)k - [(0.50 m)i + (0.75 m)j + (0.20 m)k] = (6.50m)i + (10.25m)j + (7.30m)k
Multiply this by the force vectors to calculate work.
W = Fd = [(2.00 N)i + (4.00 N)j + (6.00 N)k] × [(6.50m)i + (10.25m)j + (7.30m)k] = (13J)i + (41J)j + (43.8J)k = 97.8J
(b) To find the power of a force, divide work by time (the time we're given in the problem is 15 seconds).
P = W/Δt = 97.8J/15s = 6.52W
FINAL ANSWERS: (a) 97.8J
(b) 6.52W
(b) 6.52W
Dr. Fletcher needs to move his 2.00 kg accordion. To do this, he must apply a force F = (3.15 N)i + (7.00 N)j + (7.05 N)k so that it moves from an initial position of di = (3.15 m)i - (2.00 m)j + (5.00 m)k to a final position of df = -(5.00 m)i + (4.15 m)j + (7.00 m)k over a 4.00 s time interval.
(a) Find the work done on the accordion by the force in the 4.00 interval
(b) Find the average power provided by Dr. Fletcher during that interval.
(c) Find the angle between vectors. di and df.
(a) Find the work done on the accordion by the force in the 4.00 interval
(b) Find the average power provided by Dr. Fletcher during that interval.
(c) Find the angle between vectors. di and df.
A: (a) Find the displacement just like in the last problem:
df - di = [-(5.00 m)i + (4.15 m)j + (7.00 m)k] - [(3.15 m)i - (2.00 m)j + (5.00 m)k] = -(8.15m)i + (6.15m)j + (2.00m)k
...And then multiply by the force to find the work:
W = Fd = [(3.15 N)i + (7.00 N)j + (7.05 N)k] × [-(8.15m)i + (6.15m)j + (2.00m)k] = -(25.6725J)i + (43.05J)j + (14.1J)k = 31.4775J
(b) Now divide by time to find the power:
P = W/Δt = (31.4775J)/(4.00s) = 7.86938W
(c) Finding the angle between two 3-dimensional angles isn't as fun as when the angles are only in an xy plane, but it's still doable with the dot product (we wouldn't use the cross product for this since that only really applies when we're trying to find a vector normal to the plane containing two other vectors). Let's take the dot product with our variables and set it equal to theta:
|di||df|cosθ = didf ⇒ θ = cos-1[(didf)/(|di||df|)]
Now, let's plug in our values for this. I won't show the math for this because in text form that much math just looks like a massive hard-to-follow mess, but if you're having trouble with this equation then just remember that for the top bit, you're only multiplying the bits with like unit vectors by each other (i.e. [3.15m]i times [-5.00m]i), while the "absolute value" of a vector is just the square root of the sum of the squares of its components. The value you should get is 79.4109 degrees.
df - di = [-(5.00 m)i + (4.15 m)j + (7.00 m)k] - [(3.15 m)i - (2.00 m)j + (5.00 m)k] = -(8.15m)i + (6.15m)j + (2.00m)k
...And then multiply by the force to find the work:
W = Fd = [(3.15 N)i + (7.00 N)j + (7.05 N)k] × [-(8.15m)i + (6.15m)j + (2.00m)k] = -(25.6725J)i + (43.05J)j + (14.1J)k = 31.4775J
(b) Now divide by time to find the power:
P = W/Δt = (31.4775J)/(4.00s) = 7.86938W
(c) Finding the angle between two 3-dimensional angles isn't as fun as when the angles are only in an xy plane, but it's still doable with the dot product (we wouldn't use the cross product for this since that only really applies when we're trying to find a vector normal to the plane containing two other vectors). Let's take the dot product with our variables and set it equal to theta:
|di||df|cosθ = didf ⇒ θ = cos-1[(didf)/(|di||df|)]
Now, let's plug in our values for this. I won't show the math for this because in text form that much math just looks like a massive hard-to-follow mess, but if you're having trouble with this equation then just remember that for the top bit, you're only multiplying the bits with like unit vectors by each other (i.e. [3.15m]i times [-5.00m]i), while the "absolute value" of a vector is just the square root of the sum of the squares of its components. The value you should get is 79.4109 degrees.
FINAL ANSWERS: (a) 31.4775J
(b) 7.86938W
(c) 79.4109°
(b) 7.86938W
(c) 79.4109°
A 240 g block is dropped onto a relaxed vertical spring that has a spring constant of k = 2.2 N/cm. The block becomes attached to the spring and compresses the spring 13 cm before momentarily stopping.
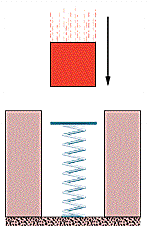
(a) While the spring is being compressed, what work is done on the block by the gravitational force on it?
(b) What work is done on the block by the spring force while the spring is being compressed?
(c) What is the speed of the block just before it hits the spring? (Assume that friction is negligible.)
(d) If the speed at impact is doubled, what is the maximum compression of the spring?

(a) While the spring is being compressed, what work is done on the block by the gravitational force on it?
(b) What work is done on the block by the spring force while the spring is being compressed?
(c) What is the speed of the block just before it hits the spring? (Assume that friction is negligible.)
(d) If the speed at impact is doubled, what is the maximum compression of the spring?
A: (a) Gravitational work is equal to the force times distance as per usual, so let's plug in our values. Note that 240g = .24kg and 13cm = 0.13m.
W = Fd = mad = (0.24kg)(9.81m/s2)(0.13m) = 0.306072J
(b) Now let's solve for work/change in energy a second time, but using the elactic potential energy formula this time.
-(1/2)kx2 = -(1/2)(220N/m)(0.13)2 = -1.859J
(c) The energy of the block at the spring's most compressed point is equal to the difference between the work due to gravity and the work on the spring.
Wg - Ws = 0.306072J - 1.859J = -1.55293J
This is the total energy of the system at the most compressed point, since we're ignoring the effects of friction. Before the block lands on the spring, KE would be the only energy in the system, so let's set this equal to the KE formula.
-1.55293J = -(1/2)mv2 = v = sqrt[2(1.55293J)/(0.24kg)] = 3.59737m/s
(d) Set the negative KE equal to the sum of the works done by gravity and the spring, and we'll find that this results in a square of the distance travelled:
v1 = 2v0 = 2(3.59737m/s)
-(1/2)mv12 = Wg + Ws = mgd1 - (1/2)kd12 ⇒ d12 - (2mg/k)d1 - mv12/k = 0
Plug these values into a quadratic equation, and take the positive root. That's our answer.
W = Fd = mad = (0.24kg)(9.81m/s2)(0.13m) = 0.306072J
(b) Now let's solve for work/change in energy a second time, but using the elactic potential energy formula this time.
-(1/2)kx2 = -(1/2)(220N/m)(0.13)2 = -1.859J
(c) The energy of the block at the spring's most compressed point is equal to the difference between the work due to gravity and the work on the spring.
Wg - Ws = 0.306072J - 1.859J = -1.55293J
This is the total energy of the system at the most compressed point, since we're ignoring the effects of friction. Before the block lands on the spring, KE would be the only energy in the system, so let's set this equal to the KE formula.
-1.55293J = -(1/2)mv2 = v = sqrt[2(1.55293J)/(0.24kg)] = 3.59737m/s
(d) Set the negative KE equal to the sum of the works done by gravity and the spring, and we'll find that this results in a square of the distance travelled:
v1 = 2v0 = 2(3.59737m/s)
-(1/2)mv12 = Wg + Ws = mgd1 - (1/2)kd12 ⇒ d12 - (2mg/k)d1 - mv12/k = 0
Plug these values into a quadratic equation, and take the positive root. That's our answer.
FINAL ANSWERS: (a) .306072J
(b) -1.859J
(c) 3.59737m/s
(d) .248577m
(b) -1.859J
(c) 3.59737m/s
(d) .248577m
In the figure below, a cord runs around two massless, frictionless pulleys. A canister with mass m = 13 kg hangs from one pulley, and you exert a force vector F on the free end of the cord. (Hint: When a cord loops around a pulley as shown, it pulls on the pulley with a net force that is twice the tension in the cord.)
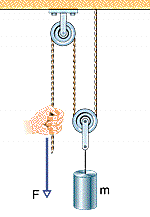
(a) What must be the magnitude of vector F if you are to lift the canister at a constant speed?
(b) To lift the canister by 1.1 cm, how far must you pull the free end of the cord?
(c) During that lift, what is the work done on the canister by your force (via the cord)?
(d) What is the work done on the canister by the gravitational force on the canister?

(a) What must be the magnitude of vector F if you are to lift the canister at a constant speed?
(b) To lift the canister by 1.1 cm, how far must you pull the free end of the cord?
(c) During that lift, what is the work done on the canister by your force (via the cord)?
(d) What is the work done on the canister by the gravitational force on the canister?
A: (a) If the cannister is being lifted at constant speed, then the net force is zero. Let's set a formula for this, and remember that two pulleys being used here means that the tension will be doubled:
Fnet = 0 = 2T - mg ⇒ T = (mg)/2 = (13kg)(9.81m/s2)/2 = 63.765N
(b) To raise the mass by a distance in a situation with two pulleys, the two segments of the cord must both be shortened by that amount. Therefore, we'll have to pull double that distance. 2(1.1cm) = 2.2cm.
(c) Our force times the distance (in meters).
W = Fd = (63.765N)(0.022m) = 1.40283J
(d) The work done by gravity is just opposite to the work we're applying to it, which won't change because the weight's motion is still the same. Therefore, the answer here is just the negative of our answer to part c.
Fnet = 0 = 2T - mg ⇒ T = (mg)/2 = (13kg)(9.81m/s2)/2 = 63.765N
(b) To raise the mass by a distance in a situation with two pulleys, the two segments of the cord must both be shortened by that amount. Therefore, we'll have to pull double that distance. 2(1.1cm) = 2.2cm.
(c) Our force times the distance (in meters).
W = Fd = (63.765N)(0.022m) = 1.40283J
(d) The work done by gravity is just opposite to the work we're applying to it, which won't change because the weight's motion is still the same. Therefore, the answer here is just the negative of our answer to part c.
FINAL ANSWERS: (a) 63.765N
(b) 2.2cm
(c) 1.40283J
(d) -1.40283J
(b) 2.2cm
(c) 1.40283J
(d) -1.40283J
A 240 kg crate hangs from the end of a rope of length L = 10.0 m. You push horizontally on the crate with a varying force F to move it 4.00 m to the side.
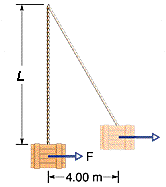
(a) What is the magnitude of F when the crate is in this final position?
(b) During the crate's displacement, what is the total work done on it?
(c) During the crate's displacement, what is the work done by the weight of the crate?
(d) During the crate's displacement, what is the work done by the pull on the crate from the rope?
(e) Knowing that the crate is motionless before and after its displacement, use the answers to (b), (c), and (d) to find the work your force F does on the crate.
(f) Why is the work of your force not equal to the product of the horizontal displacement and the answer to (a)?

(a) What is the magnitude of F when the crate is in this final position?
(b) During the crate's displacement, what is the total work done on it?
(c) During the crate's displacement, what is the work done by the weight of the crate?
(d) During the crate's displacement, what is the work done by the pull on the crate from the rope?
(e) Knowing that the crate is motionless before and after its displacement, use the answers to (b), (c), and (d) to find the work your force F does on the crate.
(f) Why is the work of your force not equal to the product of the horizontal displacement and the answer to (a)?
A: (a) The force acting on the block acting on the block will be equal to the horizontal magnitude of the rope's tension. In order to calculate this, we need both the magnitude of the total tension in the rope and the angle of the rope from the vertical at the pushed position. First, let's find the angle:
θ = sin-1(4/10) = 23.5782°
We can use this to find the total tension within the rope. Let's write a force equation for the object at the pushed position and solve for θ:
Fnet = 0 = Tcosθ - mg ⇒ Tcosθ = mg ⇒ T = (mg)/(cosθ) = (240kg)(9.81m/s2)/cos(23.5782°) = 2568.86N
Now let's use what we've learned to find the force:
Tsinθ = 2568.86Nsin23.5782° = 1027.54N.
(b) The keyword here is the word "total". This part is not asking for the work done by any particular part of the object, it's asking for the net work done on the object during the motion. Since the object begins at rest and ends at rest, there is no total change in kinetic energy and subsequently no total work.
(c) Solve for gravitational work using the Fd formula. Keep in mind that the d/h value for height raised is equal to (L - Lcosθ), or L(1 - cosθ), since we're not actually given the value for the raised height and have to derive it ourselves in terms of the length of the string and the angle at which it's raised.
W = Fd = mgh = mgL(1 - cosθ) = (240kg)(-9.81m/s2)10(1 - cos23.5782°) = -1965.57J.
Remember to keep it negative, since gravity does negative work on the system. Also, WebAssign wants the answer in kJ for some reason, so be sure to make that conversion as well.
(d) Because the object rotates upwards on a string, the rope is exerting a centripetal force on the box. As explained earlier, centripetal forces do zero work on their objects.
(e) The sum of all the works acting on the box will add up to the total work we calculated in part (b). Let's just write a simple formula for this...
Fapplied + 0kJ - 1.96557kJ = 0kJ ⇒ Fapplied = 1.96557kJ
(f) The question refers to F as a "varying force". Because the horizontal force is not constant, the standard work formula W = Fd will not apply.
θ = sin-1(4/10) = 23.5782°
We can use this to find the total tension within the rope. Let's write a force equation for the object at the pushed position and solve for θ:
Fnet = 0 = Tcosθ - mg ⇒ Tcosθ = mg ⇒ T = (mg)/(cosθ) = (240kg)(9.81m/s2)/cos(23.5782°) = 2568.86N
Now let's use what we've learned to find the force:
Tsinθ = 2568.86Nsin23.5782° = 1027.54N.
(b) The keyword here is the word "total". This part is not asking for the work done by any particular part of the object, it's asking for the net work done on the object during the motion. Since the object begins at rest and ends at rest, there is no total change in kinetic energy and subsequently no total work.
(c) Solve for gravitational work using the Fd formula. Keep in mind that the d/h value for height raised is equal to (L - Lcosθ), or L(1 - cosθ), since we're not actually given the value for the raised height and have to derive it ourselves in terms of the length of the string and the angle at which it's raised.
W = Fd = mgh = mgL(1 - cosθ) = (240kg)(-9.81m/s2)10(1 - cos23.5782°) = -1965.57J.
Remember to keep it negative, since gravity does negative work on the system. Also, WebAssign wants the answer in kJ for some reason, so be sure to make that conversion as well.
(d) Because the object rotates upwards on a string, the rope is exerting a centripetal force on the box. As explained earlier, centripetal forces do zero work on their objects.
(e) The sum of all the works acting on the box will add up to the total work we calculated in part (b). Let's just write a simple formula for this...
Fapplied + 0kJ - 1.96557kJ = 0kJ ⇒ Fapplied = 1.96557kJ
(f) The question refers to F as a "varying force". Because the horizontal force is not constant, the standard work formula W = Fd will not apply.
FINAL ANSWERS: (a) 1027.54N
(b) 0J
(c) -1.96557kJ
(d) 0J
(e) 1.96557kJ
(f) The question refers to F as a "varying force". Because the horizontal force is not constant, the standard work formula W = Fd will not apply.
(b) 0J
(c) -1.96557kJ
(d) 0J
(e) 1.96557kJ
(f) The question refers to F as a "varying force". Because the horizontal force is not constant, the standard work formula W = Fd will not apply.