Gauss' Law for Magnetic Fields
•1. The magnetic flux through each of five faces of a die (singular of “dice”) is given by ΦB = ±N Wb, where N (= 1 to 5) is the number of spots on the face.
The flux is positive (outward) for N even and negative (inward) for N odd. What is the flux through the sixth face of the die?
A: First of all, realize that the net magnetic flux through a closed surface will always be equal to zero; meaning that if we were to take the sum of the flux that passes through each face of the die, we should
find a net flux of zero. We can use a sum (and simple arithmetic) to find ΦB6, the magnetic flux through the sixth face:
Σ5N=1 -1NΦBN + ΦB6 = 0
This summation comes from the fact that face 1 will be negative (due to the fact that it's odd, and the problem tells us that odd numbers of faces are negative), with the "power of N" causing the signs to alternate (so that even numbers of faces will be positive). We use N for ΦN, so that each value in the sequence is made into the proper integers:
Σ5N=1 -1NN + Φ6 = 0
Of course, all of this is just a formal way to set up the sequence. Ultimately, you should end up with a sum that looks like this:
(- 1 Wb + 2 Wb - 3 Wb + Wb - 5 Wb) + ΦB6 = 0
- 3 Wb + ΦB6 = 0
ΦB6 = + 3 Wb
Σ5N=1 -1NΦBN + ΦB6 = 0
This summation comes from the fact that face 1 will be negative (due to the fact that it's odd, and the problem tells us that odd numbers of faces are negative), with the "power of N" causing the signs to alternate (so that even numbers of faces will be positive). We use N for ΦN, so that each value in the sequence is made into the proper integers:
Σ5N=1 -1NN + Φ6 = 0
Of course, all of this is just a formal way to set up the sequence. Ultimately, you should end up with a sum that looks like this:
(- 1 Wb + 2 Wb - 3 Wb + Wb - 5 Wb) + ΦB6 = 0
- 3 Wb + ΦB6 = 0
ΦB6 = + 3 Wb
FINAL ANSWER: + 3 Wb
•2. Figure 32-27 shows a closed surface. Along the flat top face, which has a radius of 2.0 cm, a perpendicular magnetic field B of magnitude 0.30 T is directed outward.
Along the flat bottom face, a magnetic flux of 0.70 mWb is directed outward. What are the (a) magnitude and (b) direction (inward or outward) of the magnetic flux through the
curved part of the surface?
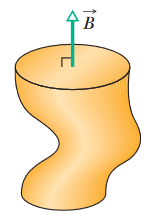

A: Remember that the net magnetic flux through a Gaussian surface must be zero. In other words,
Φbottom + Φtop + Φcurved = 0
We're given Φbottom by the problem, and Φtop = +(BA) = +(Bπr2) = +(0.30 T)π(0.020 m)2 = +0.00038 Wb = +0.38 mWb. We know it's positive because the diagram makes it clear that this field is directed "outward" from the surface. By this same logic, Φbottom should be positive as well (since the problem tells us that Φbottom is directed outward).
+ 0.70 mWb + 0.377 mWb + Φcurved = 0
+ 1.1 mWb + Φcurved = 0
Φcurved = -1.1 mWb
This result tells us both the magnitude and the direction of the flux through the curved surface. The fact that the result is negative means that the flux must be direction inward.
Φbottom + Φtop + Φcurved = 0
We're given Φbottom by the problem, and Φtop = +(BA) = +(Bπr2) = +(0.30 T)π(0.020 m)2 = +0.00038 Wb = +0.38 mWb. We know it's positive because the diagram makes it clear that this field is directed "outward" from the surface. By this same logic, Φbottom should be positive as well (since the problem tells us that Φbottom is directed outward).
+ 0.70 mWb + 0.377 mWb + Φcurved = 0
+ 1.1 mWb + Φcurved = 0
Φcurved = -1.1 mWb
This result tells us both the magnitude and the direction of the flux through the curved surface. The fact that the result is negative means that the flux must be direction inward.
FINAL ANSWERS: (a) 1.1 mWb
(b) Inward
(b) Inward
••3. A Gaussian surface in the shape of a right circular cylinder with end caps has a radius of 12.0 cm and a length of 80.0 cm. Through one end there is an inward magnetic flux of
25.0 μWb. At the other end there is a uniform magnetic field of 1.60 mT, normal to the surface and directed outward. What are the (a) magnitude and (b) direction (inward or outward) of the net magnetic flux
through the curved surface?
A: Gauss' law for magnetism is expressed as ∮B•dA = 0. Let's define Φ1 is the flux through the first end, Φ2 is the flux through the second end, and ΦC
is the flux through the "curved" side of the cylinder. Since the sum of all these components of the flux should equal zero, we can expand this as:
∮B•dA = Φ1 + Φ2 + ΦC = 0.
We're solving for ΦC.
ΦC = - Φ1 - Φ2
We're told that Φ1 has a magnitude of 25.0 μWb, but because it's directed inward, it should be negative - So Φ1 = -25.0 μWb. We must also solve for Φ2.
Φ2 = BA = (1.60 x 10-3 T)π(0.120 m)2 = + 7.24 x 10-5 Wb = + 72.4 μWb.
Now apply this information to solve for ΦC.
ΦC = - Φ1 - Φ2 = - (-25.0 μWb) - (+ 72.4 μWb) = 25.0 μWb - 72.4 μWb = - 47.4 μWb
Because the flux has a negative sign, it must be directed inwards into the Gaussian surface.
∮B•dA = Φ1 + Φ2 + ΦC = 0.
We're solving for ΦC.
ΦC = - Φ1 - Φ2
We're told that Φ1 has a magnitude of 25.0 μWb, but because it's directed inward, it should be negative - So Φ1 = -25.0 μWb. We must also solve for Φ2.
Φ2 = BA = (1.60 x 10-3 T)π(0.120 m)2 = + 7.24 x 10-5 Wb = + 72.4 μWb.
Now apply this information to solve for ΦC.
ΦC = - Φ1 - Φ2 = - (-25.0 μWb) - (+ 72.4 μWb) = 25.0 μWb - 72.4 μWb = - 47.4 μWb
Because the flux has a negative sign, it must be directed inwards into the Gaussian surface.
FINAL ANSWERS: (a) |ΦC| = 47.4 μWb
(b) Inward through the curved surface.
(b) Inward through the curved surface.
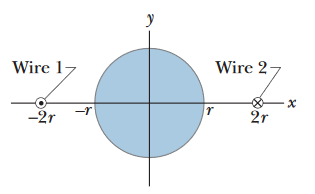
•••4. Two wires, parellel to a z axis and a distance 4r apart, carry equal currents i in opposite directions, as shown in Fig. 32-28. A circular cylinder of radius r and length L has its
axis on the z axis, midway between the wires. Use Gauss’ law for magnetism to derive an expression for the net outward magnetic flux through the half of the cylindrical surface above the x axis.
(Hint: Find the flux through the portion of the xz plane that lies within the cylinder.)