Faraday's Law and Lenz's Law
•1. In Fig. 30-33, a circular loop of wire 10 cm in diameter (seen edge-on) is placed with its normal N at an angle θ = 30° with the direction of a uniform magnetic field B of magnitude
0.50 T. The loop is then rotated such that N rotates in a cone about the field direction at the rate 100 rev/min; angle θ remains unchanged during the process. What is the emf induced in the loop?
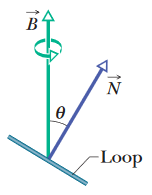

A: The induced electromotive force, or emf, is given as ℰ = -dΦB/dt. In other words, it's the rate of change of the magnetic flux through the loop with respect to time. However,
if we look carefully at the problem, there doesn't seem to be a change in the flux with respect to time. The magnetic flux is the dot product of the magnetic field and the area vector of the loop, or:
ΦB = B•A = BAcosθ
However, notice that the problem describes the magnetic field as "uniform" and the diameter of the loop is given to us as constant as well. Not only that, but the problem also explicitly tells us that the angle θ is completely unchanging. Everything about this situation tells us that the magnetic flux won't actually be changing at all, so the derivative mentioned earlier should be equal to zero; that is to say, there is no emf induced in the loop.
ΦB = B•A = BAcosθ
However, notice that the problem describes the magnetic field as "uniform" and the diameter of the loop is given to us as constant as well. Not only that, but the problem also explicitly tells us that the angle θ is completely unchanging. Everything about this situation tells us that the magnetic flux won't actually be changing at all, so the derivative mentioned earlier should be equal to zero; that is to say, there is no emf induced in the loop.
FINAL ANSWER: zero
•2. A certain elastic conducting material is stretched into a circular loop of 12.0 cm radius. It is placed with its plane perpendicular to a uniform 0.800 T magnetic field. When released, the radius
of the loop starts to shrink at an instantaneous rate of 75.0 cm/s. What emf is induced in the loop at that instant?
A: We use the formula for Faraday's law to find the induced emf, taking into account the area of a circle as A = πr2.
ℰ = -dΦB/dt = -d(BA)/dt = -B*dA/dt = -B*d(πr2)/dt
We then differentiate implicitly:
-2πrB*dr/dt = -2π(0.12 m)(0.800 T)(-0.750 m/s) = 0.452 V
ℰ = -dΦB/dt = -d(BA)/dt = -B*dA/dt = -B*d(πr2)/dt
We then differentiate implicitly:
-2πrB*dr/dt = -2π(0.12 m)(0.800 T)(-0.750 m/s) = 0.452 V
FINAL ANSWER: 0.452 V
•3. In Fig. 30-34, a 120-turn coil of radius 1.8 cm and resistance 5.3 Ω is coaxial with a solenoid of 220 turns/cm and diameter 3.2 cm. The solenoid current drops from 1.5 A to zero
in time interval Δt = 25 ms. What current is induced in the coil during Δt?
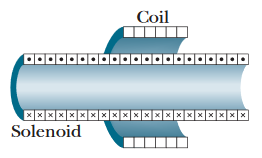

A: We're given the resistance of the coil, and emf is a type of voltage - this means that if we can find the emf, we'll be able to use Ohm's law to evaluate the induced current.
We first use Faraday's law to set up the emf:
ℰ = -N*dΦB/dt = -N*(d(BA)/dt) = -NA*(dB/dt)
Also note that the magnetic field inside a solenoid is given by B = μ0in, where μ0 is the permeability constant, i is the current through the solenoid, and n is the number of turns per unit length of the solenoid. For the radius "r" of the area, we use the radius of the solenoid (rather than the radius of the regular coil) because the entirety of the magnetic flux passing through the coil comes from the solenoid in this case.
ℰ = -NA*(dB/dt) = -NA(d/dt)(μ0in) = -Nμ0nA(di/dt) = -Nμ0n(πr2)(di/dt)
= -(120)(4π x 10-7 T•m/A)(22000 /m)π(0.016 m)2[(-1.5 A)/(0.025 s)] = 0.16 V.
Now let's use Ohm's law to calculate the induced current, using our emf as a type of voltage:
iind = |ℰ|/R = (0.16 V)/(5.3 Ω) = 0.030 A
ℰ = -N*dΦB/dt = -N*(d(BA)/dt) = -NA*(dB/dt)
Also note that the magnetic field inside a solenoid is given by B = μ0in, where μ0 is the permeability constant, i is the current through the solenoid, and n is the number of turns per unit length of the solenoid. For the radius "r" of the area, we use the radius of the solenoid (rather than the radius of the regular coil) because the entirety of the magnetic flux passing through the coil comes from the solenoid in this case.
ℰ = -NA*(dB/dt) = -NA(d/dt)(μ0in) = -Nμ0nA(di/dt) = -Nμ0n(πr2)(di/dt)
= -(120)(4π x 10-7 T•m/A)(22000 /m)π(0.016 m)2[(-1.5 A)/(0.025 s)] = 0.16 V.
Now let's use Ohm's law to calculate the induced current, using our emf as a type of voltage:
iind = |ℰ|/R = (0.16 V)/(5.3 Ω) = 0.030 A
FINAL ANSWER: 0.030 A
•4. A wire loop of radius 12 cm and resistance 8.5 Ω is located in a uniform magnetic field B that changes in magnitude as given in Fig. 30-35. The vertical axis scale is set by
Bs = 0.50 T, and the horizontal axis scale is set by ts = 6.00 s. The loop’s plane is perpendicular to B. What emf is induced in the loop during time intervals (a) 0 to 2.0 s,
(b) 2.0 s to 4.0 s, and (c) 4.0 s to 6.0 s?
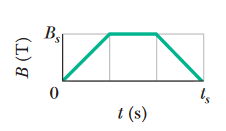

A: (a) We use Faraday's law:
ℰ = -dΦB/dt = -πr2*dB/dt = -π(0.12 m)2[(0.5 T)/(2.0 s)] = -1.1 x 10-2 V
(b) From the second interval (2 to 4 seconds), the magnetic field is a straight horizontal line (in other words, the magnetic field is constant). This means that the magnetic flux through the wire loop isn't changing, and as such, there will be no induced emf through the loop. So the answer here is zero.
(c) We use Faraday's law:
ℰ = -dΦB/dt = -πr2*dB/dt = -π(0.12 m)2[(-0.5 T)/(6.0 s - 4.0 s)] = 1.1 x 10-2 V
ℰ = -dΦB/dt = -πr2*dB/dt = -π(0.12 m)2[(0.5 T)/(2.0 s)] = -1.1 x 10-2 V
(b) From the second interval (2 to 4 seconds), the magnetic field is a straight horizontal line (in other words, the magnetic field is constant). This means that the magnetic flux through the wire loop isn't changing, and as such, there will be no induced emf through the loop. So the answer here is zero.
(c) We use Faraday's law:
ℰ = -dΦB/dt = -πr2*dB/dt = -π(0.12 m)2[(-0.5 T)/(6.0 s - 4.0 s)] = 1.1 x 10-2 V
FINAL ANSWERS: (a) -1.1 x 10-2 V
(b) zero
(c) -1.1 x 10-2 V
(b) zero
(c) -1.1 x 10-2 V