This chapter covers vectors, resolving vectors into their components, unit vectors, vector addition, and vector multiplication (including dot products and cross products).
Personally, I feel that this textbook's handling of dot/cross products is a bit rushed and sloppy, so I recommend coming equipped with knowledge of multivariable/vector
calculus before taking on this chapter.
Vectors and Their Components
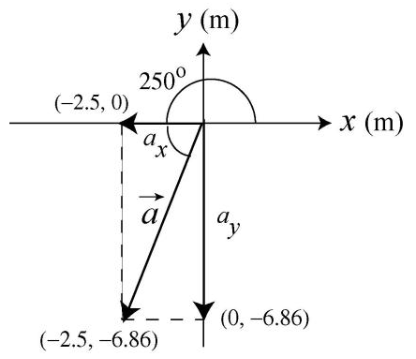
•1. What are (a) the x component and (b) the y component of a vector "a" in the xy plane if its direction is 250° counterclockwise from the positive direction
of the x axis and its magnitude is 7.3 m?
A: The x and y components of the vector a are given by
ax = a*cosθ & ay = a*sinθ
...where a is the magnitude of the vector. We can plug the magnitude and the angle into these formulas to find each component.
(a) ax = (7.3 m)cos250° = -2.5 m
(b) ay = (7.3 m)sin250° = -6.86 m ≈ -6.9 m
The final vector, and its components, look like this:
ax = a*cosθ & ay = a*sinθ
...where a is the magnitude of the vector. We can plug the magnitude and the angle into these formulas to find each component.
(a) ax = (7.3 m)cos250° = -2.5 m
(b) ay = (7.3 m)sin250° = -6.86 m ≈ -6.9 m
The final vector, and its components, look like this:

FINAL ANSWERS: (a) -2.5 m
(b) -6.9 m
(b) -6.9 m
•2. A displacement vector "r" in the xy plane is 15 m long and directed at angle θ = 30° in Fig. 3-26. Determine (a) the x component and (b) the y component of the vector.

A: (a) The x component of the vector is
rx = r*cosθ = (15 m)cos30° = 13 m
(b) The y component of the vector is
ry = r*sinθ = (15 m)sin30° = 7.5 m
rx = r*cosθ = (15 m)cos30° = 13 m
(b) The y component of the vector is
ry = r*sinθ = (15 m)sin30° = 7.5 m
FINAL ANSWERS: (a) 13 m
(b) 7.5 m
(b) 7.5 m
•3. The x component of vector "A" is -25.0 m and the y component is +40.0 m. (a) What is the magnitude of "A"? (b) What is the angle between the direction of "A" and
the positive direction of x?
A: (a) When vectors are given in terms of their "components" (the magnitude of the x direction, the magnitude of the y direction, etc), you might notice that all these components are at right angles
to one another. This means that we can represent a straight magnitude using Pythagorean's theorem. If each component and the resultant vector are looked at together as a right triangle, then we can represent this
as
A2 = Ax2 + Ay2 --> A = sqrt[Ax2 + Ay2]
= sqrt[(-25.0 m)2 + (40.0 m)2] = 47.2 m
(b) Finding the angle is trickier, because technically there are numerous "correct" answers. We find an angle based on components by using the inverse tangent:
tan-1[Ay/Ax] = tan-1[(40.0 m)/(-25.0 m)] = -58°
However, due to the way the tangent function works, tanθ = tanθ + n180°, where "n" is any positive integer number. This means that there could be a few possible answers to this. In a situation like this, it's best to draw a graph of the components and the resultant vector, to see where the vector will lie.

We can clearly see from this image that the vector lies in the second quadrant, somewhere between 90° and 180° from the positive x axis - our true answer must be in that range. Adding 180° to -58° gets us 122°, so that must be the angle.
(b) Finding the angle is trickier, because technically there are numerous "correct" answers. We find an angle based on components by using the inverse tangent:
tan-1[Ay/Ax] = tan-1[(40.0 m)/(-25.0 m)] = -58°
However, due to the way the tangent function works, tanθ = tanθ + n180°, where "n" is any positive integer number. This means that there could be a few possible answers to this. In a situation like this, it's best to draw a graph of the components and the resultant vector, to see where the vector will lie.

We can clearly see from this image that the vector lies in the second quadrant, somewhere between 90° and 180° from the positive x axis - our true answer must be in that range. Adding 180° to -58° gets us 122°, so that must be the angle.
FINAL ANSWERS: (a) 47.2 m
(b) 122°
(b) 122°
•4. Express the following angles in radians: (a) 20.0°, (b) 50.0°, (c) 100°. Convert the following angles to degrees: (d) 0.330 rad, (e) 2.10 rad, (f) 7.70 rad.
A: A full circle is 360° = 2π radians, so that's the conversion factor we use (I personally like to use 180° = π rad, since it's slightly simpler).
(a) (20.0°)(π rad / 180°) = 0.349 rad
(b) (50.0°)(π rad / 180°) = 0.873 rad
(c) (100°)(π rad / 180°) = 1.75 rad
(d) (0.330 rad)(180° / π rad) = 18.9°
(e) (2.10 rad)(180° / π rad) = 120°
(f) (7.70 rad)(180° / π rad) = 441°
(a) (20.0°)(π rad / 180°) = 0.349 rad
(b) (50.0°)(π rad / 180°) = 0.873 rad
(c) (100°)(π rad / 180°) = 1.75 rad
(d) (0.330 rad)(180° / π rad) = 18.9°
(e) (2.10 rad)(180° / π rad) = 120°
(f) (7.70 rad)(180° / π rad) = 441°
FINAL ANSWERS: I mean. They're pretty much already laid out nice and neatly above, so why should I bother rewriting them?
•5. A ship sets out to sail to a point 120 km due north. An unexpected storm blows the ship to a point 100 km due east of its starting point. (a) How far and
(b) in what direction must it now sail to reach its original destination?
A: Since the ship has been blown 100 km east, it must now travel both 120 km north and 100 km west (-100 km, taking "east" to be the positive x direction) to get to its intended definition.
We use the Pythagorean theorem to find the total distance.
d = sqrt[(-100 km)2 + (120 km)2] = 156 km
We find the angle from the positive x axis by taking the tangent of the y component divided by the x component.
tan-1[(120 km)/(-100 km)] = -50.2°
We know from the geometry of the problem that the vector must be pointed in the second quadrant, so we add 180° to get 129.8°. This means 129.8° north of east. We can write this in a slightly more meaningful / easy-to-understand way by subtracting 90° from this, so we can write it as 39.8° west of north.
d = sqrt[(-100 km)2 + (120 km)2] = 156 km
We find the angle from the positive x axis by taking the tangent of the y component divided by the x component.
tan-1[(120 km)/(-100 km)] = -50.2°
We know from the geometry of the problem that the vector must be pointed in the second quadrant, so we add 180° to get 129.8°. This means 129.8° north of east. We can write this in a slightly more meaningful / easy-to-understand way by subtracting 90° from this, so we can write it as 39.8° west of north.
FINAL ANSWERS: (a) 156 km
(b) 39.8° west of north
(b) 39.8° west of north
•6. In Fig. 3-27, a heavy piece of machinery is raised by sliding it a distance d = 12.5 m along a plank oriented at angle θ = 20.0° to the horizontal. How far is it moved
(a) vertically and (b) horizontally?
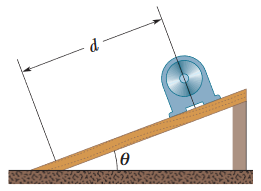

A: We can represent the motion of the machinery in terms of "horizontally" and "vertically" by using the trig functions to find the components of its displacement.
(a) The vertical height is dsinθ = (12.5 m)sin(20.0°) = 4.28 m
(b) The horizontal distance is dcosθ = (12.5 m)cos(20.0°) = 11.7 m
(a) The vertical height is dsinθ = (12.5 m)sin(20.0°) = 4.28 m
(b) The horizontal distance is dcosθ = (12.5 m)cos(20.0°) = 11.7 m
FINAL ANSWERS: (a) 4.28 m
(b) 11.7 m
(b) 11.7 m
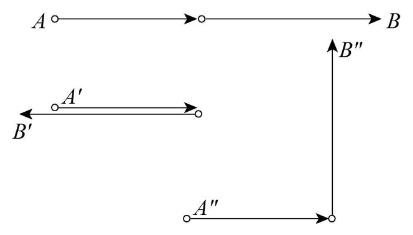
•7. Consider two displacements, one of magnitude 3 m and another of magnitude 4 m. Show how the displacement vectors may be combined to get a resultant displacement of magnitude
(a) 7 m, (b) 1 m, and (c) 5 m.
A: (a) Since 7 m is the sum of 3 m and 4 m, this magnitude can only be the resultant vector if the two vectors are parellel and are being added together.
3 m + 4 m = 7 m
(b) Since the resultant displacement in this case is smaller than both individual displacements, they must be pointing in opposite directions. More specifically, they must be anti-parallel in this case.
4 m + (-3 m) = 1 m
(c) The resultant is greater than each individual component, but less than the total sum of them both. Therefore, the components must be roughly perpendicular to one another. In this case, they must be completely perpendicular.
sqrt[32 + 42] = 5 m
3 m + 4 m = 7 m
(b) Since the resultant displacement in this case is smaller than both individual displacements, they must be pointing in opposite directions. More specifically, they must be anti-parallel in this case.
4 m + (-3 m) = 1 m
(c) The resultant is greater than each individual component, but less than the total sum of them both. Therefore, the components must be roughly perpendicular to one another. In this case, they must be completely perpendicular.
sqrt[32 + 42] = 5 m

FINAL ANSWERS: (a) The sum of two parallel vectors
(b) The sum of two anti-parallel vectors
(c) The sum of two orthogonal vectors
(b) The sum of two anti-parallel vectors
(c) The sum of two orthogonal vectors
Unit Vectors, Adding Vectors by Components
•8. A person walks in the following pattern: 3.1 km north, then 2.4 km west, and finally 5.2 km south. (a) Sketch the vector diagram that represents this motion. (b) How far and
(c) in what direction would a bird fly in a straight line from the same starting point to the same final point?
A: (a) We can draw the diagram like this:
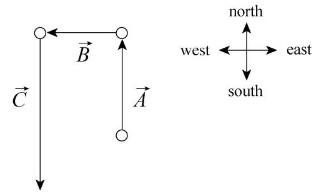
Where the vectors are A = (3.1 km)j, B = (-2.4 km)i, and C = (-5.2 km)j.
(b) The "straight line" from the start point to the final point is the displacement of the person throughout their entire walk. We can find the displacement vector by adding up all the vector components we found.
r = A + B + C = (-2.4 km)i + (-2.1 km)j
|r| = sqrt[(-2.4 km)2 + (-2.1 km)2] ≈ 3.2 km
(c) θ = tan-1 [(-2.1 km)/(-2.4 km)] = 41°, or 221° counterclockwise from the positive x axis. We choose 221°, because the displacement vector must be in the third quadrant in this case (as per the diagram above). More efficiently, this can be written as 41° south from west, or 49° west from south.

Where the vectors are A = (3.1 km)j, B = (-2.4 km)i, and C = (-5.2 km)j.
(b) The "straight line" from the start point to the final point is the displacement of the person throughout their entire walk. We can find the displacement vector by adding up all the vector components we found.
r = A + B + C = (-2.4 km)i + (-2.1 km)j
|r| = sqrt[(-2.4 km)2 + (-2.1 km)2] ≈ 3.2 km
(c) θ = tan-1 [(-2.1 km)/(-2.4 km)] = 41°, or 221° counterclockwise from the positive x axis. We choose 221°, because the displacement vector must be in the third quadrant in this case (as per the diagram above). More efficiently, this can be written as 41° south from west, or 49° west from south.
FINAL ANSWERS: (a) See diagram above.
(b) 3.2 km
(c) 49° west of south
(b) 3.2 km
(c) 49° west of south
•9. Two vectors are given by
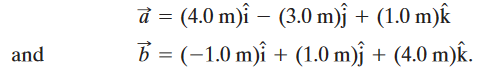
In unit-vector notation, find (a) a + b, (b) a - b, and (c) a third vector such that a - b + c = 0.
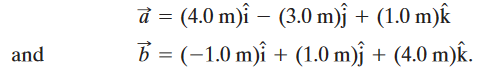
In unit-vector notation, find (a) a + b, (b) a - b, and (c) a third vector such that a - b + c = 0.
A: To find the vector sums, we add the individual components together.
(a) a + b = [4.0 + (-1.0)]i + [(-3.0) + 1.0]j + (1.0 + 4.0)k = (3.0i - 2.0j + 5.0k) m
(b) a - b = [4.0 - (-1.0)]i + [(-3.0) - 1.0]j + (1.0 - 4.0)k = (5.0i - 4.0j - 3.0k) m
(c) If a - b + c = 0, then c must equal b - a, so that all the terms cancel out. This means that c will actually be the negative of what we found in part (b); (-5.0i + 4.0j + 3.0k) m.
(a) a + b = [4.0 + (-1.0)]i + [(-3.0) + 1.0]j + (1.0 + 4.0)k = (3.0i - 2.0j + 5.0k) m
(b) a - b = [4.0 - (-1.0)]i + [(-3.0) - 1.0]j + (1.0 - 4.0)k = (5.0i - 4.0j - 3.0k) m
(c) If a - b + c = 0, then c must equal b - a, so that all the terms cancel out. This means that c will actually be the negative of what we found in part (b); (-5.0i + 4.0j + 3.0k) m.
FINAL ANSWERS: (a) (3.0i - 2.0j + 5.0k) m
(b) (5.0i - 4.0j - 3.0k) m
(c) (-5.0i + 4.0j + 3.0k) m.
(b) (5.0i - 4.0j - 3.0k) m
(c) (-5.0i + 4.0j + 3.0k) m.
•10. Find the (a) x, (b) y, and (c) z components of the sum r of the displacements c and d whose components in meters are cx = 7.4, cy = -3.8,
cz = -6.1; dx = 4.4, dy = -2.0, dz = 3.3.
A: We add the relevant components of each vector together, pretty easily enough.
(a) rx = cx + dx = 7.4 m + 4.4 m = 12 m
(b) ry = cy + dy = -3.8 m - 2.0 m = -5.8 m
(c) rz = cz + dz = -6.1 m + 3.3 m = -2.8 m
(a) rx = cx + dx = 7.4 m + 4.4 m = 12 m
(b) ry = cy + dy = -3.8 m - 2.0 m = -5.8 m
(c) rz = cz + dz = -6.1 m + 3.3 m = -2.8 m
FINAL ANSWERS: (a) 12 m
(b) -5.8 m
(c) -2.8 m
(b) -5.8 m
(c) -2.8 m
•11. (a) In unit-vector notation, what is the sum a + b if a = (4.0 m)i + (3.0 m)j and b = (-13.0 m)i + (7.0 m)j? What are the
(b) magnitude and (c) direction of a + b?
A: (a) We add vectors by adding the individual components given for each vector.
rx = ax + bx = (4.0 m) + (-13 m) = -9.0 m
ry = ay + by = (3.0 m) + (7.0 m) = 10.0 m
r = (-9.0 m)i + (10 m)j
(b) The magnitude of r is |r| = sqrt[rx2 + ry2] = sqrt[(-9.0 m)2 + (10 m)2] = 13 m
(c) θ = tan-1 [ry/rx] = tan-1 [(10.0 m)/(-9.0 m)] = -48° or 132°
Because the x component of the resultant vector is negative, and the y component is positive, the vector must be directed in the second quadrant - so we choose the latter option for the angle.
rx = ax + bx = (4.0 m) + (-13 m) = -9.0 m
ry = ay + by = (3.0 m) + (7.0 m) = 10.0 m
r = (-9.0 m)i + (10 m)j
(b) The magnitude of r is |r| = sqrt[rx2 + ry2] = sqrt[(-9.0 m)2 + (10 m)2] = 13 m
(c) θ = tan-1 [ry/rx] = tan-1 [(10.0 m)/(-9.0 m)] = -48° or 132°
Because the x component of the resultant vector is negative, and the y component is positive, the vector must be directed in the second quadrant - so we choose the latter option for the angle.
FINAL ANSWERS: (a) (-9.0 m)i + (10 m)j
(b) 13 m
(c) 132° counterclockwise from the positive x axis
(b) 13 m
(c) 132° counterclockwise from the positive x axis
•12. A car is driven east for a distance of 50 km, then north for 30 km, and then in a direction 30° east of north for 25 km. Sketch the vector diagram and determine (a) the magnitude and
(b) the angle of the car’s total displacement from its starting point.
A: Let's sketch a vector diagram of this situation:
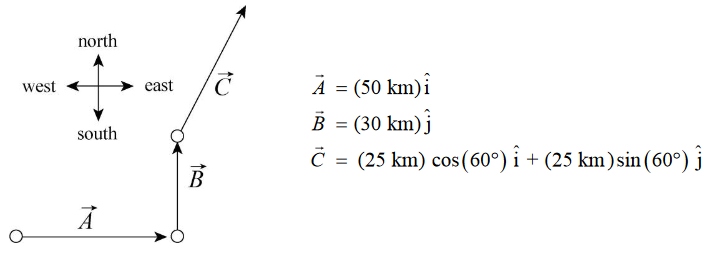
(a) Adding the vectors together:
r = A + B + C = (62.5 km)i + (51.7 km)j
|r| = sqrt[(62.5 km)2 + (51.7 km)2] = 81 km
(b) θ = tan-1 [(51.7 km)/(62.5 km)] = 40° north of east

(a) Adding the vectors together:
r = A + B + C = (62.5 km)i + (51.7 km)j
|r| = sqrt[(62.5 km)2 + (51.7 km)2] = 81 km
(b) θ = tan-1 [(51.7 km)/(62.5 km)] = 40° north of east
FINAL ANSWERS: (a) 81 km
(b) 40° north of east
(b) 40° north of east
•13. A person desires to reach a point that is 3.40 km from her present location and in a direction that is 35.0° north of east. However, she must travel along streets that are
oriented either north – south or east – west. What is the minimum distance she could travel to reach her destination?
A: The total distance of displacement is equal to the sum of its individual components, in terms of the sinusoidal functions.
distance = dcosθ + dsinθ = (3.40 km)cos35.0° + (3.40 km)sin35.0° = 4.74 km
distance = dcosθ + dsinθ = (3.40 km)cos35.0° + (3.40 km)sin35.0° = 4.74 km
FINAL ANSWER: 4.74 km
•14. You are to make four straight-line moves over a flat desert floor, starting at the origin of an xy coordinate system and ending at the xy coordinates (-140 m, 30 m). The x component and y
component of your moves are the following, respectively, in meters: (20 and 60), then (bx and -70), then (-20 and cy), then (-60 and -70). What are (a) component bx and
(b) component cy? What are (c) the magnitude and (d) the angle (relative to the positive direction of the x axis) of the overall displacement?
A: (a) Sum up the x components of the coordinates.
20 m + bx - 20 m - 60 m = -140 m --> bx = -80 m
(b) Sum up the y components of the coordinates.
60 m - 70 m + cy - 70 m = 30 m --> cy = 110 m
(c) The magnitude is found with the Pythagorean theorem.
sqrt[(-140 m)2 + (30 m)2] ≈ 143 m
(d) θ = tan-1 [30/(-140)] = -12° clockwise from the -x axis, or 168° counterclockwise from the +x axis.
20 m + bx - 20 m - 60 m = -140 m --> bx = -80 m
(b) Sum up the y components of the coordinates.
60 m - 70 m + cy - 70 m = 30 m --> cy = 110 m
(c) The magnitude is found with the Pythagorean theorem.
sqrt[(-140 m)2 + (30 m)2] ≈ 143 m
(d) θ = tan-1 [30/(-140)] = -12° clockwise from the -x axis, or 168° counterclockwise from the +x axis.
FINAL ANSWERS: (a) -80 m
(b) 110 m
(c) 143 m
(d) 168° counterclockwise from the +x axis.
(b) 110 m
(c) 143 m
(d) 168° counterclockwise from the +x axis.
•15. The two vectors a and b in Fig. 3-28 have equal magnitudes of 10.0 m and the angles are θ1 = 30° and θ2 = 105°. Find the (a) x and (b) y components
of their vector sum r, (c) the magnitude of r, and (d) the angle makes with the positive direction of the xaxis.
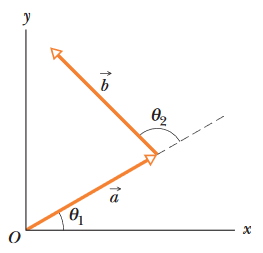

A: The vector sum r should look like this:
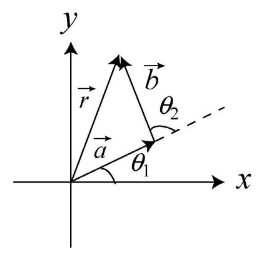
(a) We add the x components together, adding both angles for vector b.
rx = acosθ1 + bcos(θ1 + θ2) = (10 m)cos30° + (10 m)cos(30° + 105°) = 1.59 m
(b) ry = asinθ1 + bsin(θ1 + θ2) = (10 m)sin30° + (10 m)sin(30° + 105°) = 12.1 m
(c) Now we perform a vector sum on these two components.
|r| = sqrt[(1.59 m)2 + (12.1 m)2] = 12.2 m
(d) θ = tan-1 [ry/rx] = tan-1 [(12.1 m)/(1.59 m)] = 82.5°

(a) We add the x components together, adding both angles for vector b.
rx = acosθ1 + bcos(θ1 + θ2) = (10 m)cos30° + (10 m)cos(30° + 105°) = 1.59 m
(b) ry = asinθ1 + bsin(θ1 + θ2) = (10 m)sin30° + (10 m)sin(30° + 105°) = 12.1 m
(c) Now we perform a vector sum on these two components.
|r| = sqrt[(1.59 m)2 + (12.1 m)2] = 12.2 m
(d) θ = tan-1 [ry/rx] = tan-1 [(12.1 m)/(1.59 m)] = 82.5°
FINAL ANSWERS: (a) 1.59 m
(b) 12.1 m
(c) 82.5°
(b) 12.1 m
(c) 82.5°
•16. For the displacement vectors a = (3.0 m)i + (4.0 m)j and b = (5.0 m)i + (-2.0 m)j, give a + b in (a) unit-vector notation, and as (b) a magnitude and (c) an angle (relative to i). Now give
b - a in (d) unit-vector notation, and as (e) a magnitude and (f) an angle.
A: (a) Add the vectors together:
(3.0i + 4.0j) m + (5.0i - 2.0j) m = (8.0 m)i + (2.0 m)j
(b) |a + b| = sqrt[(8.0 m)2 + (2.0 m)2] = 8.2 m
(c) θ = tan-1 [(2.0 m)/(8.0 m)] = 14°
(d) b - a = (5.0i - 2.0j) m - (3.0i + 4.0j) m = (2.0 m)i - (6.0 m)j
(e) |b - a| = sqrt[(2.0 m)2 + (-6.0 m)2] = 6.3 m
(f) θ = tan-1 [(-6.0 m)/(2.0 m)] = -72°
(3.0i + 4.0j) m + (5.0i - 2.0j) m = (8.0 m)i + (2.0 m)j
(b) |a + b| = sqrt[(8.0 m)2 + (2.0 m)2] = 8.2 m
(c) θ = tan-1 [(2.0 m)/(8.0 m)] = 14°
(d) b - a = (5.0i - 2.0j) m - (3.0i + 4.0j) m = (2.0 m)i - (6.0 m)j
(e) |b - a| = sqrt[(2.0 m)2 + (-6.0 m)2] = 6.3 m
(f) θ = tan-1 [(-6.0 m)/(2.0 m)] = -72°
FINAL ANSWERS: (a) (8.0 m)i + (2.0 m)j
(b) 8.2 m
(c) 14°
(d) (2.0 m)i - (6.0 m)j
(e) 6.3 m
(f) -72°
(b) 8.2 m
(c) 14°
(d) (2.0 m)i - (6.0 m)j
(e) 6.3 m
(f) -72°
•17. Three vectors a, b, and c each have a magnitude of 50 m and lie in an xy plane. Their directions relative to the positive direction of the x axis are 30°, 195°, and 315°, respectively.
What are (a) the magnitude and (b) the angle of the vector a + b + c, and (c) the magnitude and (d) the angle of a - b + c? What are the (e) magnitude and (f) angle of a fourth vector d such that
(a + b) - (c + d) = 0?
A:
FINAL ANSWERS:
Multiplying Vectors
•33. For the vectors in Fig. 3-32, with a = 4, b = 3, and c = 5, what are (a) the magnitude and (b) the direction of a × b, (c) the magnitude and
(d) the direction of a × c, and (e) the magnitude and (f) the direction of b × c? (The z axis is not shown.)
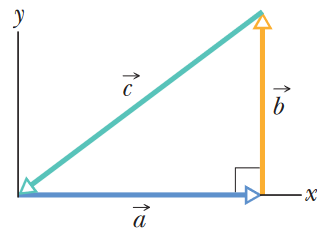

A: (a) Finding the magnitude of the cross product is pretty easy here, since we're given the magnitudes of each vector, and we can determine the angles
fairly quickly from the diagram shown. Thus, we can use the cross product formula in its simplest form:
a*b*sin(ϕ) = (4)(3)sin(90°) = (4)(3) = 12 (Note that sin(90°) = 1, so we can simplify the sine out of the formula.)
(b) With cross products, the direction of the resulting vector can be found using the right-hand rule. Imagine that the vectors a and b originate from the same point, and curl your fingers from vector a to vector b through the shortest distance between them. Your thumb will point in the direction of the resulting vector. In this case, the resulting direction should be out of the page/screen towards you, or the +z direction.
(c) We have the magnitude of the individual vectors, but it's a little harder to find the angle between the relevant vectors. This time around, we'll have to use the trigonometric functions, which are applicable since the vectors form a right triangle together. Remember, we're looking for sin(ϕ), where ϕ is the angle between vectors a and c. The sine of an angle is defined as the triangle's side opposite to that angle, divided by the hypotenuse (longest side) of the triangle. All of this considered, sin(ϕ) = 3/5, as those are the magnitudes of the relevant vectors. We apply this to the cross product formula:
a*c*sin(ϕ) = (4)(5)sin(ϕ) = (4)(5)(3/5) = 12
(d) We apply the right-hand rule as in (b). This time, we should find that the direction of the resulting vector is into the page, or in the -z direction.
(e) Like in part (c), we'll need to use the trig functions to rewrite sin(ϕ) as a ratio of the triangle's sides. Since we need the angle between vectors b and c, sin(ϕ) is equal to 4/5.
b*c*sin(ϕ) = (3)(5)sin(ϕ) = (3)(5)(4/5) = 12
(f) Applying the right-hand rule a third time, we find that the resulting vector is in the +z direction, out of the page.
a*b*sin(ϕ) = (4)(3)sin(90°) = (4)(3) = 12 (Note that sin(90°) = 1, so we can simplify the sine out of the formula.)
(b) With cross products, the direction of the resulting vector can be found using the right-hand rule. Imagine that the vectors a and b originate from the same point, and curl your fingers from vector a to vector b through the shortest distance between them. Your thumb will point in the direction of the resulting vector. In this case, the resulting direction should be out of the page/screen towards you, or the +z direction.
(c) We have the magnitude of the individual vectors, but it's a little harder to find the angle between the relevant vectors. This time around, we'll have to use the trigonometric functions, which are applicable since the vectors form a right triangle together. Remember, we're looking for sin(ϕ), where ϕ is the angle between vectors a and c. The sine of an angle is defined as the triangle's side opposite to that angle, divided by the hypotenuse (longest side) of the triangle. All of this considered, sin(ϕ) = 3/5, as those are the magnitudes of the relevant vectors. We apply this to the cross product formula:
a*c*sin(ϕ) = (4)(5)sin(ϕ) = (4)(5)(3/5) = 12
(d) We apply the right-hand rule as in (b). This time, we should find that the direction of the resulting vector is into the page, or in the -z direction.
(e) Like in part (c), we'll need to use the trig functions to rewrite sin(ϕ) as a ratio of the triangle's sides. Since we need the angle between vectors b and c, sin(ϕ) is equal to 4/5.
b*c*sin(ϕ) = (3)(5)sin(ϕ) = (3)(5)(4/5) = 12
(f) Applying the right-hand rule a third time, we find that the resulting vector is in the +z direction, out of the page.
FINAL ANSWERS: (a) 12
(b) +z direction
(c) 12
(d) -z direction
(e) 12
(f) +z direction
(b) +z direction
(c) 12
(d) -z direction
(e) 12
(f) +z direction
•34. Two vectors are presented as a = 3.0i + 5.0j and b = 2.0i + 4.0j. Find (a) a × b, (b) a • b, (c) (a + b) • b, and (d) the component of a along the direction
of b. (Hint: for (d), consider Eq. 3-20 and Fig. 3-18.)
A: Parts (a) - (c) are all just trivial applications of the given methods for vector multiplication/addition.
(a) a × b = (axby - aybx)k = [(3.0)(4.0) - (5.0)(2.0)]k = 2.0k
(b) a • b = axbx + ayby = (3.0)(2.0) + (5.0)(4.0) = 26
(c) (a + b) • b = ((3.0 + 2.0)i + (5.0 + 4.0)j) • (2.0i + 4.0j) = (5.0i + 9.0j) • (2.0i + 4.0j) = (5.0)(2.0) + (9.0)(4.0) = 46
(d) The "component of a vector along the direction of another vector" is something that's known as the scalar projection, and it's taught in multivariable/vector calculus courses. The formula for it (in the case of projecting vector a onto vector b) is a*cosθ, or a • b / ||b||. Since we calculated the dot product of a and b in part (b), we can simply take our answer to that part and divide it by the absolute value of b.
||b|| = 2*sqrt(5) (Found using the Pythagorean theorem)
26 / [2*sqrt(5)] = 5.8
(a) a × b = (axby - aybx)k = [(3.0)(4.0) - (5.0)(2.0)]k = 2.0k
(b) a • b = axbx + ayby = (3.0)(2.0) + (5.0)(4.0) = 26
(c) (a + b) • b = ((3.0 + 2.0)i + (5.0 + 4.0)j) • (2.0i + 4.0j) = (5.0i + 9.0j) • (2.0i + 4.0j) = (5.0)(2.0) + (9.0)(4.0) = 46
(d) The "component of a vector along the direction of another vector" is something that's known as the scalar projection, and it's taught in multivariable/vector calculus courses. The formula for it (in the case of projecting vector a onto vector b) is a*cosθ, or a • b / ||b||. Since we calculated the dot product of a and b in part (b), we can simply take our answer to that part and divide it by the absolute value of b.
||b|| = 2*sqrt(5) (Found using the Pythagorean theorem)
26 / [2*sqrt(5)] = 5.8
FINAL ANSWERS: (a) 2.0k
(b) 26
(c) 46
(d) 5.8
(b) 26
(c) 46
(d) 5.8