This chapter covers Gauss' law (the first of Maxwell's equations), electric flux, and miscellaneous applications of Gauss' law.
If you would like me to go over a certain problem, please email your requests to kevinbarbuto@gmail.com.
Problems
Electric Flux
•1. The square surface shown in Fig. 23-30 measures 3.2 mm on each side. It is immersed in a uniform electric field
with magnitude E = 1800 N/C and with field lines at an angle of θ = 35° with a normal to the surface, as shown. Take that normal to be directed
“outward,” as though the surface were one face of a box. Calculate the electric flux through the surface.
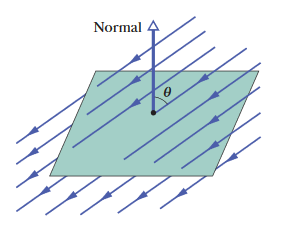

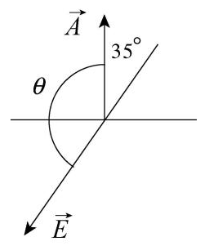
A: The flux acts through the surface at an angle to the area vector normal to the square surface. A slightly more clear way to visualize it is this:
Now recall that an amount of flux through a Gaussian surface, Φ, is generally represented by the integral of the dot product of the electric field and area vectors. That is,
Φ = ∫E•dA
However, the magnitude of the electric field is considered to be "constant" in this case, so there's nothing to integrate here - we can more simply represent the formula for the flux as a single dot product:
Φ = E•A = EAcosθ.
Where θ is the smallest angle between the "positive-pointing" sides of the area and electric field vectors (recall that the flux is maximized when both vectors point in the same direction). From the diagram above, we can infer that the angle θ will be 180° - 35° = 145°. We can use this angle in our formula for the flux, squaring the side length of the square for the area of the surface.
Φ = EAcosθ = (1800 N/C)(3.2 x 10-3 m)2cos145° = -1.5 x 10-2 N•m2/C.

Now recall that an amount of flux through a Gaussian surface, Φ, is generally represented by the integral of the dot product of the electric field and area vectors. That is,
Φ = ∫E•dA
However, the magnitude of the electric field is considered to be "constant" in this case, so there's nothing to integrate here - we can more simply represent the formula for the flux as a single dot product:
Φ = E•A = EAcosθ.
Where θ is the smallest angle between the "positive-pointing" sides of the area and electric field vectors (recall that the flux is maximized when both vectors point in the same direction). From the diagram above, we can infer that the angle θ will be 180° - 35° = 145°. We can use this angle in our formula for the flux, squaring the side length of the square for the area of the surface.
Φ = EAcosθ = (1800 N/C)(3.2 x 10-3 m)2cos145° = -1.5 x 10-2 N•m2/C.
FINAL ANSWER: -1.5 x 10-2 N•m2/C
••2. An electric field given by E = 4.0i - 3.0(y2 + 2.0)j pierces a Gaussian cube of edge length 2.0 m
and positioned as shown in Fig. 23-7. (The magnitude E is in newtons per coulomb and the position x is in meters.) What is the electric flux
through the (a) top face, (b) bottom face, (c) left face, and (d) back face? (e) What is the net electric flux through the cube?
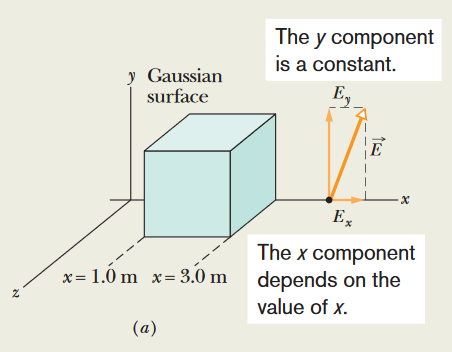
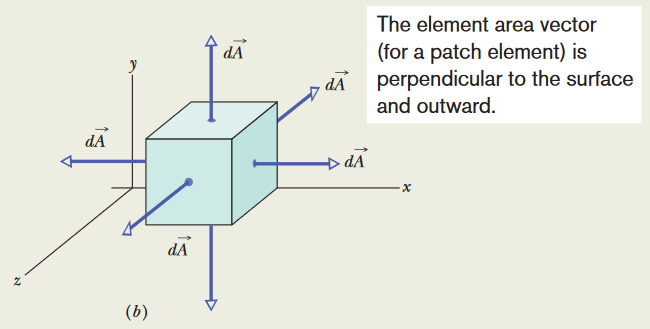


A: To find the electric flux at any point on the Gaussian surface, especially with a variable electric field, we use the integral Φ = ∮E•dA (using the "loop" integral symbol in this case
because the Gaussian surface is a closed surface in this case). We can use the information we have about various points on the cube to find the flux through each face.
(a) For the top face, we can tell that the entire top face is positioned at y = 2.0 m. Since our formula for the electric field is in terms of y, we can find the electric field using this information.
E = 4.0i - 3.0((2.0)2 + 2.0)j = 4.0i - 18j.
Also, because the dA area vector is directed upwards from the top face of the top face, we can represent dA as a unit vector as (dA)j. Now we apply the dot product integral to find the flux:
Φ = ∫topE•dA = ∫top(4.0i - 18j)•(dA)j = -18∫topdA = (-18)(2.0)2 N•m2/C = -72 N•m2/C
(b) For the bottom face, y = 0 on these coordinates, and dA = -(dA)j, because the area vector is pointed downwards. The electric field we find is then:
E = 4.0i - 3.0((0)2 + 2.0)j = 4.0i - 6j.
Now use this to calculate the flux:
Φ = ∫bottomE•dA = ∫bottom(4.0i - 6j)•(dA)(-j) = 6∫bottomdA = 6(2.0)2 N•m2/C = +24 N•m2/C
(c) For the left face of the cube, there is no fixed y component we can use, meaning that we won't find a single value for the electric field. However, this ends up not being an issue, since the area vector for the cube's left face is dA = -(dA)i (pointing leftward), so the y component of the electric field ends up being ignored in the dot product for flux:
Φ = ∫leftE•dA = Φ = ∫left(4i + Eyj)•(dA)(-i) = -4∫leftdA = -4(2.0)2N•m2/C = -16 N•m2/C
(d) The area vector on the back face of the cube points in the negative z direction; dA = (dA)(-k). However, looking at the formula we have for electric field, there is only an x component and a y component. Due to the nature of the dot product, E•dA = 0 and there will be no flux through the back face. This same idea can be applied to the front face of the cube.
(e) The net flux through the cube is equal to the sum of the flux through each face. It's important to realize that the front face will have the same flux as the back face, because the area vectors associated with both form a dot product with the electric field of zero. It's also important to know that the flux travelling "out" through the right face of the cube will be positive, as opposed to the negative flux through the left side of the cube; this is because of the nature of the dot product: any flux travelling "into" a Gaussian surface is negative, and the flux travelling "out" of a Gaussian surface is positive. The left and right sides will also both have the same magnitude of flux through them (16 N•m2/C), because the vector formula for the electric field here doesn't change on either surface. The net flux through the cube is then:
Φ = (-72 + 24 - 16 + 0 + 0 + 16) = -48 N•m2/C
(a) For the top face, we can tell that the entire top face is positioned at y = 2.0 m. Since our formula for the electric field is in terms of y, we can find the electric field using this information.
E = 4.0i - 3.0((2.0)2 + 2.0)j = 4.0i - 18j.
Also, because the dA area vector is directed upwards from the top face of the top face, we can represent dA as a unit vector as (dA)j. Now we apply the dot product integral to find the flux:
Φ = ∫topE•dA = ∫top(4.0i - 18j)•(dA)j = -18∫topdA = (-18)(2.0)2 N•m2/C = -72 N•m2/C
(b) For the bottom face, y = 0 on these coordinates, and dA = -(dA)j, because the area vector is pointed downwards. The electric field we find is then:
E = 4.0i - 3.0((0)2 + 2.0)j = 4.0i - 6j.
Now use this to calculate the flux:
Φ = ∫bottomE•dA = ∫bottom(4.0i - 6j)•(dA)(-j) = 6∫bottomdA = 6(2.0)2 N•m2/C = +24 N•m2/C
(c) For the left face of the cube, there is no fixed y component we can use, meaning that we won't find a single value for the electric field. However, this ends up not being an issue, since the area vector for the cube's left face is dA = -(dA)i (pointing leftward), so the y component of the electric field ends up being ignored in the dot product for flux:
Φ = ∫leftE•dA = Φ = ∫left(4i + Eyj)•(dA)(-i) = -4∫leftdA = -4(2.0)2N•m2/C = -16 N•m2/C
(d) The area vector on the back face of the cube points in the negative z direction; dA = (dA)(-k). However, looking at the formula we have for electric field, there is only an x component and a y component. Due to the nature of the dot product, E•dA = 0 and there will be no flux through the back face. This same idea can be applied to the front face of the cube.
(e) The net flux through the cube is equal to the sum of the flux through each face. It's important to realize that the front face will have the same flux as the back face, because the area vectors associated with both form a dot product with the electric field of zero. It's also important to know that the flux travelling "out" through the right face of the cube will be positive, as opposed to the negative flux through the left side of the cube; this is because of the nature of the dot product: any flux travelling "into" a Gaussian surface is negative, and the flux travelling "out" of a Gaussian surface is positive. The left and right sides will also both have the same magnitude of flux through them (16 N•m2/C), because the vector formula for the electric field here doesn't change on either surface. The net flux through the cube is then:
Φ = (-72 + 24 - 16 + 0 + 0 + 16) = -48 N•m2/C
FINAL ANSWERS: (a) -72 N•m2/C
(b) +24 N•m2/C
(c) -16 N•m2/C
(d) 0
(e) -48 N•m2/C
(b) +24 N•m2/C
(c) -16 N•m2/C
(d) 0
(e) -48 N•m2/C
••3. The cube in Fig. 23-31 has edge length 1.40 m and is oriented as shown in a region of uniform electric field. Find the electric flux through the right face if
the electric field, in newtons per coulomb, is given by (a) 6.00i, (b) -2.00 j, and (c) -3.00i + 4.00k. (d) What is the total flux through the cube for each field?
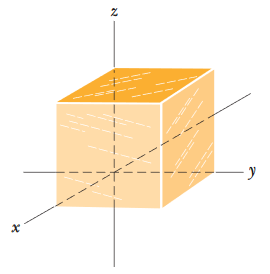

A: Because our electric fields in this case aren't variable, we can use the simpler formula for electric flux of Φ = E•A. The "right face" points in the y direction based on the diagram,
so A = Aj = (1.40 m)2j. Now we just use the electric field we're given for each part of the problem.
(a) Φ = (6.00 N/C)i•(1.40 m)2j = 0 (It turns out to be zero because of the dot product.)
(b) Φ = (-2.00 N/C)j•(1.40 m)2j = -3.92 N•m2/C
(c) Φ = [(-3.00 N/C)i + (4.00 N/C)k]•(1.40 m)2j = 0
(d) In all three cases, the electric field is always uniform - none of its components are variable, and the magnitude of the field doesn't change with its distance from a point. Because the electric field is uniform and passes through the entire cube, and because the cube is a closed surface, the same amount of field that enters the cube and leaves through the other side. This is a general rule: The total flux of a uniform field that passes through a closed surface is always zero. This applies to all three cases.
(a) Φ = (6.00 N/C)i•(1.40 m)2j = 0 (It turns out to be zero because of the dot product.)
(b) Φ = (-2.00 N/C)j•(1.40 m)2j = -3.92 N•m2/C
(c) Φ = [(-3.00 N/C)i + (4.00 N/C)k]•(1.40 m)2j = 0
(d) In all three cases, the electric field is always uniform - none of its components are variable, and the magnitude of the field doesn't change with its distance from a point. Because the electric field is uniform and passes through the entire cube, and because the cube is a closed surface, the same amount of field that enters the cube and leaves through the other side. This is a general rule: The total flux of a uniform field that passes through a closed surface is always zero. This applies to all three cases.
FINAL ANSWERS: (a) 0
(b) -3.92 N•m2/C
(c) 0
(d) 0, for every field
(b) -3.92 N•m2/C
(c) 0
(d) 0, for every field
Gauss' Law
•4. In Fig. 23-32, a butterfly net is in a uniform electric field of magnitude E = 3.0 mN/C. The rim, a circle of radius a = 11 cm, is aligned perpendicular to the field. The net contains no net charge.
Find the electric flux through the netting.
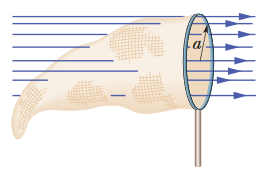

A: You would be right to notice that the "opening" of the ring makes this not a closed surface, but there is language written in the problem which suggests that we are to assume that it is anyway (that is,
we're supposed to treat the shape as though there is a flat "surface" across the ring section of the net).
The fact that there is "no net charge" contained within the ring and netting means that the net flux that travels through the entire net-ring system must be equal to zero.
If some amount of flux is exiting the net-ring system through the ring, then an amount of equal magnitude is entering through the netting. We can calculate the amount of
flux exiting the system through the ring using the formula:
Φ = EA = E*πa2 = (3.0 x 10-3 N/C)*π(0.11 m)2 = 1.1 x 10-4 N•m2/C
This is the amount of flux passing through the ring. The problem asks us for the flux that passes through the net. Because the flux is essentially "entering" the system when it passes through the net, this should be negative:
Φ' = -Φ = -1.1 x 10-4 N•m2/C
Φ = EA = E*πa2 = (3.0 x 10-3 N/C)*π(0.11 m)2 = 1.1 x 10-4 N•m2/C
This is the amount of flux passing through the ring. The problem asks us for the flux that passes through the net. Because the flux is essentially "entering" the system when it passes through the net, this should be negative:
Φ' = -Φ = -1.1 x 10-4 N•m2/C
FINAL ANSWER: -1.1 x 10-4 N•m2/C
•5. In Fig. 23-33, a proton is a distance d/2 directly above the center of a square of side d. What is the magnitude of the electric flux through the square? (Hint: Think of the square
as one face of a cube with edge d.)
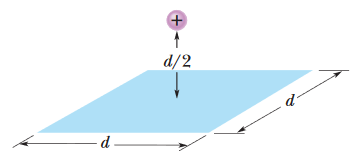

A: According to Gauss' law, a charged particle "enclosed" by a Gaussian surface has its charge related to the electric flux passing through the surface, by ε0Φ = qenc.
The flux can then be found by solving for Φ, and getting Φ = qenc/ε0.
In this case, however, the charge clearly isn't being enclosed by a Gaussian surface, but if we take advantage of the problem's symmetry, then we can pretend that it is and work from there.
Imagine that there are five other squares (identical to the one that's already there) encasing the proton, so that there are six total squares forming a cube with the proton at the center. In this scenario, we really do have a closed surface through which the proton is sending some electric flux, and the flux through the cube really does follow Φ = qenc/ε0. Of course, this doesn't reflect the reality of the situation, but imagining the situation like this makes it clear that the actual flux through the single square will be one sixth of what it would be if all six of those hypothetical squares were there (since the actual electric field only passes through one of those six squares). We reflect that in our formula:
Φ = qenc/[6ε0] = (1.6 x 10-19 C)/[(6)(8.85 x 10-12 C2/N•m2)] = 3.01 x 10-9 N•m2/C
Imagine that there are five other squares (identical to the one that's already there) encasing the proton, so that there are six total squares forming a cube with the proton at the center. In this scenario, we really do have a closed surface through which the proton is sending some electric flux, and the flux through the cube really does follow Φ = qenc/ε0. Of course, this doesn't reflect the reality of the situation, but imagining the situation like this makes it clear that the actual flux through the single square will be one sixth of what it would be if all six of those hypothetical squares were there (since the actual electric field only passes through one of those six squares). We reflect that in our formula:
Φ = qenc/[6ε0] = (1.6 x 10-19 C)/[(6)(8.85 x 10-12 C2/N•m2)] = 3.01 x 10-9 N•m2/C
FINAL ANSWER: 3.01 x 10-9 N•m2/C
•6. At each point on the surface of the cube shown in Fig. 23-31, the electric field is parallel to the z axis. The length of each edge of the cube is 3.0 m. On the top face of the
cube the field is E = -34k N/C, and on the bottom face it is E = +20k N/C. Determine the net charge contained within the cube.


A: We have some amount of flux travelling through the top and bottom faces of the cube. At the top face, the field is negative and travelling into the cube. At the bottom face, the field is positive
and travelling into the cube. Both fields are directed into the cube, so the enclosed charge must be negative. We can use the basic formula for flux (Φ = EAcosθ = EA, where θ = 0) to find the flux through the top
and bottom faces of the cube.
|Φtop| = EA = (34 N/C)(3.0 m)2 = 306 N•m2/C (this flux is directed inward, so it's actually negative)
|Φbottom| = EA = (20 N/C)(3.0 m)2 = 180 N•m2/C (this flux is also negative because of how it's directed inward)
Φtotal = Φtop + Φbottom = -306 N•m2/C - 180 N•m2/C = -486 N•m2/C
We can now use Gauss' law to find the enclosed charge.
qenc = ε0Φ = (8.85 x 10-12 C2/N•m2)(- 486 N•m2/C) = -4.3 x 10-9 C
|Φtop| = EA = (34 N/C)(3.0 m)2 = 306 N•m2/C (this flux is directed inward, so it's actually negative)
|Φbottom| = EA = (20 N/C)(3.0 m)2 = 180 N•m2/C (this flux is also negative because of how it's directed inward)
Φtotal = Φtop + Φbottom = -306 N•m2/C - 180 N•m2/C = -486 N•m2/C
We can now use Gauss' law to find the enclosed charge.
qenc = ε0Φ = (8.85 x 10-12 C2/N•m2)(- 486 N•m2/C) = -4.3 x 10-9 C
FINAL ANSWER: -4.3 x 10-9 C
•7. A particle of charge 1.8 μC is at the center of a Gaussian cube 55 cm on edge. What is the net electric flux through the surface?
A: We use Gauss' law to solve for the net electric flux through the cube.
Φ = q/ε0 = (1.8 x 10-6 C)/(8.85 x 10-12 C2/N•m2) = 2.0 x 105 N•m2/C
Φ = q/ε0 = (1.8 x 10-6 C)/(8.85 x 10-12 C2/N•m2) = 2.0 x 105 N•m2/C
FINAL ANSWER: 2.0 x 105 N•m2/C
A Charged Isolated Conductor
17. A uniformly charged conducting sphere of 1.2 m diameter has surface charge density 8.1 μC/m2. Find (a) the net charge on the sphere and
(b) the total electric flux leaving the surface.
A: (a) The charge on the surface of an object is equal to the surface charge density times the area, or q = σA, or q = σ(4πR2), because we're dealing with a
spherical shape in this case. Keep in mind that we're given the diameter of the sphere, we need to halve it before we can use the value for the radius.
q = (8.1 x 10-6 C/m2)4π(0.60 m)2 = 3.7 x 10-5 C
(b) We can find the flux using Gauss' law.
Φ = q/ε0 = (3.66 x 10-5 C)/(8.85 x 10-12 C2/N•m2) = 4.1 x 106 N•m2/C
q = (8.1 x 10-6 C/m2)4π(0.60 m)2 = 3.7 x 10-5 C
(b) We can find the flux using Gauss' law.
Φ = q/ε0 = (3.66 x 10-5 C)/(8.85 x 10-12 C2/N•m2) = 4.1 x 106 N•m2/C
FINAL ANSWERS: (a) 3.7 x 10-5 C
(b) 4.1 x 106 N•m2/C
(b) 4.1 x 106 N•m2/C
•18. The electric field just above the surface of the charged conducting drum of a photocopying machine has a magnitude E of 2.3 x 105 N/C. What is the surface
charge density on the drum?
A: The formula given for the magnitude of an electric field outside a conductor is E = σ/ε0. Solve for σ:
σ = Eε0 = (2.3 x 105 N/C)(8.85 x 10-12 C2/N•m2) = 2.0 x 10-6 C/m2
σ = Eε0 = (2.3 x 105 N/C)(8.85 x 10-12 C2/N•m2) = 2.0 x 10-6 C/m2
FINAL ANSWER: 2.0 x 10-6 C/m2
19. Space vehicles traveling through Earth’s radiation belts can intercept a significant number of electrons. The resulting charge buildup can damage electronic components
and disrupt operations. Suppose a spherical metal satellite 1.3 m in diameter accumulates 2.4 μC of charge in one orbital revolution. (a) Find the resulting surface charge density. (b) Calculate the
magnitude of the electric field just outside the surface of the satellite, due to the surface charge.
A: (a) Make sure you understand that a "surface charge density" is an amount of charge per unit of area, or σ = q/A, where A (the surface area of the sphere) is 4πR2,
which can be written as πD2 (D is the diameter of the sphere, which is what's given to us).
σ = q/[πD2] = (2.4 x 10-6 C)/[π(1.3 m)2] = 4.5 x 10-7 C/m2
(b) The formula for the magnitude of the electric field just outside the surface of a charged object is
E = σ/ε0 = (4.5 x 10-7 C/m2)/(8.85 x 10-12 C2/N•m2) = 5.1 x 104 N/C
σ = q/[πD2] = (2.4 x 10-6 C)/[π(1.3 m)2] = 4.5 x 10-7 C/m2
(b) The formula for the magnitude of the electric field just outside the surface of a charged object is
E = σ/ε0 = (4.5 x 10-7 C/m2)/(8.85 x 10-12 C2/N•m2) = 5.1 x 104 N/C
FINAL ANSWERS: (a) 4.5 x 10-7 C/m2
(b) 5.1 x 104 N/C
(b) 5.1 x 104 N/C
•20. Flux and conducting shells. A charged particle is held at the center of two concentric conducting spherical shells. Figure 23-39a shows a cross section. Figure 23-39b
gives the net flux Φ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere. The scale of the vertical axis is set by Φs
= 5.0 x 105 N•m2/C. What are (a) the charge of the central particle and the net charges of (b) shell A and (c) shell B?
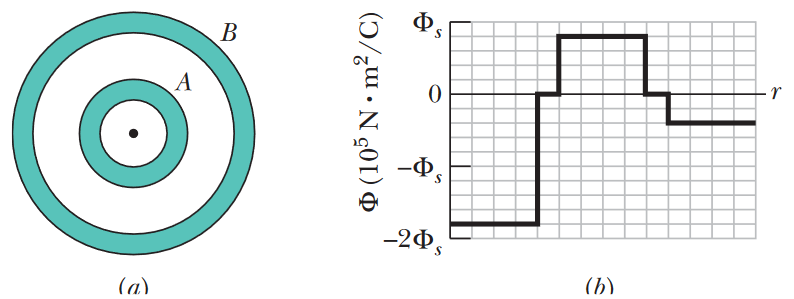
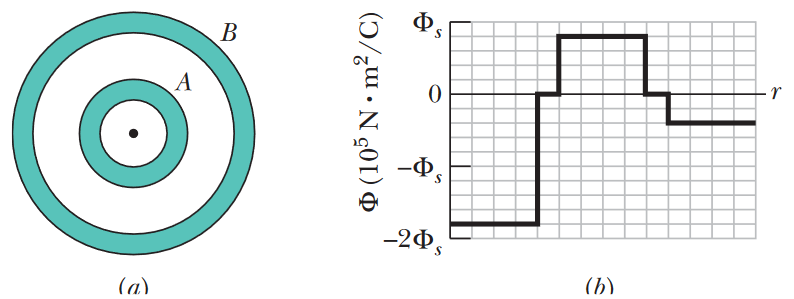
A: We use Gauss' law, ε0Φ = qenc to find the charge at each point in the system.
(a) The central particle is at the point where the radius r = 0, and according to the graph, the flux at that point is -9.0 x 105 N•m2/C. Apply Gauss' law:
qcentral = ε0Φ1 = (8.85 x 10-12 C2/N•m2)(-9.0 x 105 N•m2/C) = -7.97 x 10-6 C ≈ -8.0 μC
(b) Recall that the electric field within a conductor is almost always zero (and thus, the flux is zero too), so the points on the graph where the flux is equal to zero must be the areas where the Gaussian sphere is within the conducting shells. Therefore, we ignore these "zero" regions and focus on the next non-zero value of the flux, where the G-sphere is between the two conducting shells: +4.0 x 105 N•m2/C. Apply Gauss' law:
qenc = ε0Φ2 = (8.85 x 10-12 C2/N•m2)(+4.0 x 105 N•m2/C) = 3.54 x 10-6 C
However, the charge enclosed within this Gaussian sphere includes the charge on the central particle as well as the charge on shell A. To find the charge on shell A specifically, we subtract the charge we discovered for the central particle from this total enclosed charge.
qA = qenc - qcentral = 3.54 x 10-6 C - (-7.97 x 10-6 C) = 11.5 x 10-6 C ≈ 12 μC
(c) Now we increase the size of our Gaussian sphere once again, to surround shell B as well. The flux here (again, ignoring the next point where Φ = 0), we find that Φ3 = -2.0 x 105 N•m2/C. Apply Gauss' law:
qtotal enc = ε0Φ3 = (8.85 x 10-12 C2/N•m2)(-2.0 x 105 N•m2/C) = -1.77 x 10-6 C
This represents the total charges of the central particle and both shells combined. Just like in part (b), we subtract the irrelevant charges.
qB = qtotal enc - qA - qcentral = -1.77 x 10-6 C - 11.5 x 10-6 C - (-7.97 x 10-6 C) = -5.3 μC
(a) The central particle is at the point where the radius r = 0, and according to the graph, the flux at that point is -9.0 x 105 N•m2/C. Apply Gauss' law:
qcentral = ε0Φ1 = (8.85 x 10-12 C2/N•m2)(-9.0 x 105 N•m2/C) = -7.97 x 10-6 C ≈ -8.0 μC
(b) Recall that the electric field within a conductor is almost always zero (and thus, the flux is zero too), so the points on the graph where the flux is equal to zero must be the areas where the Gaussian sphere is within the conducting shells. Therefore, we ignore these "zero" regions and focus on the next non-zero value of the flux, where the G-sphere is between the two conducting shells: +4.0 x 105 N•m2/C. Apply Gauss' law:
qenc = ε0Φ2 = (8.85 x 10-12 C2/N•m2)(+4.0 x 105 N•m2/C) = 3.54 x 10-6 C
However, the charge enclosed within this Gaussian sphere includes the charge on the central particle as well as the charge on shell A. To find the charge on shell A specifically, we subtract the charge we discovered for the central particle from this total enclosed charge.
qA = qenc - qcentral = 3.54 x 10-6 C - (-7.97 x 10-6 C) = 11.5 x 10-6 C ≈ 12 μC
(c) Now we increase the size of our Gaussian sphere once again, to surround shell B as well. The flux here (again, ignoring the next point where Φ = 0), we find that Φ3 = -2.0 x 105 N•m2/C. Apply Gauss' law:
qtotal enc = ε0Φ3 = (8.85 x 10-12 C2/N•m2)(-2.0 x 105 N•m2/C) = -1.77 x 10-6 C
This represents the total charges of the central particle and both shells combined. Just like in part (b), we subtract the irrelevant charges.
qB = qtotal enc - qA - qcentral = -1.77 x 10-6 C - 11.5 x 10-6 C - (-7.97 x 10-6 C) = -5.3 μC
FINAL ANSWERS: (a) -8.0 μC
(b) 12 μC
(c) -5.3 μC
(b) 12 μC
(c) -5.3 μC
Applying Gauss' Law: Cylindrical Symmetry
•22. An electron is released 9.0 cm from a very long nonconducting rod with a uniform 6.0 μC/m. What is the magnitude of the electron’s initial acceleration?
A: The net force on an object is F = ma. In this case, the only force acting on the electron is a force due to an electric field, which is equal to qE. Keep in mind that the charge "q" in this case
is the elementary charge (the charge on an electron), and the electric field "E" due to a long line of charge is equal to λ/[2πε0r].
m|a| = qE = eE = eλ/[2πε0r] --> |a| = eλ/[2πε0rm] = 2.1 x 1017 m/s2
m|a| = qE = eE = eλ/[2πε0r] --> |a| = eλ/[2πε0rm] = 2.1 x 1017 m/s2
FINAL ANSWER: 2.1 x 1017 m/s2
•23. (a) The drum of a photocopying machine has a length of 42 cm and a diameter of 12 cm. The electric field just above the drum’s surface is 2.3 x 105 N/C. What is the total charge
on the drum? (b) The manufacturer wishes to produce a desktop version of the machine. This requires reducing the drum length to 28 cm and the diameter to 8.0 cm. The electric field at the drum surface must not
change. What must be the charge on this new drum?
A: (a) To find the total charge on the surface of an object, we can use the formula q = σA, where A is the side surface area on the drum (A = 2πRh = πDh), and σ is the
surface charge density on the drum (σ = ε0E).
q = σA = σπDh = πε0EDh = 3.2 x 10-7 C
(b) This can be done very easily by using the same formula that was used to solve part (a), only this time using 0.08 m instead of .12 m for the diameter, and .28 m instead of .42 m for the drum length. Doing this, we find an answer of 1.4 x 10-7 C
q = σA = σπDh = πε0EDh = 3.2 x 10-7 C
(b) This can be done very easily by using the same formula that was used to solve part (a), only this time using 0.08 m instead of .12 m for the diameter, and .28 m instead of .42 m for the drum length. Doing this, we find an answer of 1.4 x 10-7 C
FINAL ANSWERS: (a) 3.2 x 10-7 C
(b) 1.4 x 10-7 C
(b) 1.4 x 10-7 C
•24. Figure 23-40 shows a section of a long, thin-walled metal tube of radius R = 3.00 cm, with a charge per unit length of λ = 2.00 x 10-8 C/m. What is the magnitude E
of the electric field at radial distance (a) r = R/2.00 and (b) r = 2.00R? (c) Graph E versus r for the range r = 0 to 2.00R.
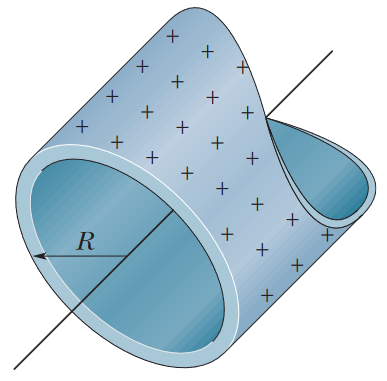

A: Even though this metal tube is a three-dimensional object, we're approximating it as a straight line of charge (hence the linear charge density given by the problem). For this problem,
we imagine a Gaussian cylinder, concentric with the tube, and we'll use this G-cylinder to analyze the electric field at various points depending on the radial distance from the central axis.
(a) In this part, our Gaussian cylinder has a radius smaller than the radius of the metal tube; this means that the Gaussian surface is enclosing no charge, and the electric field here must be zero.
(b) In this part, the radius of our Gaussian surface will be placed outside the tube, so we will be enclosing some charge here. Let's apply the formula for the electric field at a point away from a line of charge. The "r" value we use in the formula will be the distance from the center of the metal tube, in order to properly approximate the tube as a line of charge.
E = λ/[2πε0r] = (2.00 x 10-8 C/m)/[2π(8.85 x 10-12 C2/N•m2)(0.0600 m)] = 5.99 x 103 N/C
(c) This can easily be graphed with a graphing calculator, using the λ/[2πε0r] formula, plugging in all of the constants and using "r" as the input variable. When we construct our version of the graph, however, we also need to make sure that E = 0 on the domain 0 ≤ r < 0.03 m, since those are the radii at which any Gaussian surface will enclose no charge (as discussed in part (a)). Our graph looks like this:
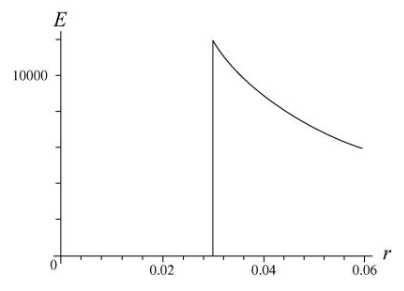
(a) In this part, our Gaussian cylinder has a radius smaller than the radius of the metal tube; this means that the Gaussian surface is enclosing no charge, and the electric field here must be zero.
(b) In this part, the radius of our Gaussian surface will be placed outside the tube, so we will be enclosing some charge here. Let's apply the formula for the electric field at a point away from a line of charge. The "r" value we use in the formula will be the distance from the center of the metal tube, in order to properly approximate the tube as a line of charge.
E = λ/[2πε0r] = (2.00 x 10-8 C/m)/[2π(8.85 x 10-12 C2/N•m2)(0.0600 m)] = 5.99 x 103 N/C
(c) This can easily be graphed with a graphing calculator, using the λ/[2πε0r] formula, plugging in all of the constants and using "r" as the input variable. When we construct our version of the graph, however, we also need to make sure that E = 0 on the domain 0 ≤ r < 0.03 m, since those are the radii at which any Gaussian surface will enclose no charge (as discussed in part (a)). Our graph looks like this:

FINAL ANSWERS: (a) Zero
(b) 5.99 x 103 N/C
(c) See graph above.
(b) 5.99 x 103 N/C
(c) See graph above.
•25. An infinite line of charge produces a field of magnitude 4.5 x 104 N/C at distance 2.0 m. Find the linear charge density.
A: The formula for the electric field at a radial distance r away from a line of charge is given by E = λ/[2πε0r]. Solve for the linear charge density λ:
E = λ/[2πε0r] --> λ = 2πε0Er = 2π(8.85 x 10-12 C2/N•m2)(4.5 x 104 N/C)(2.0 m) = 5.0 x 10-6 C/m
E = λ/[2πε0r] --> λ = 2πε0Er = 2π(8.85 x 10-12 C2/N•m2)(4.5 x 104 N/C)(2.0 m) = 5.0 x 10-6 C/m
FINAL ANSWER: 5.0 x 10-6 C/m
Applying Gauss' Law: Planar Symmetry
•33. In Fig. 23-44, two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have excess surface charge densities of opposite signs and
magnitude 7.00 x 10-22 C/m2. In unit-vector notation, what is the electric field at points (a) to the left of the plates, (b) to the right of them, and (c) between them?
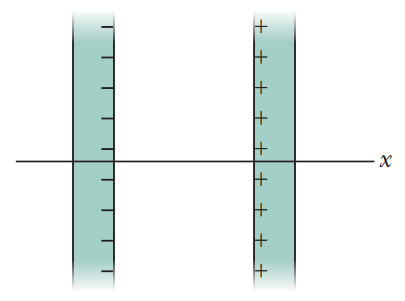

A: Since both plates have surface charge densities that are equal in magnitude and opposite in sign, our knowledge of electric field lines tells us that all the field that comes from the positively
charged plate should entirely dissipate at the negatively charged plate. Intuitively, this should tell us that there is zero electric field both to the left and to the right of the plates.
Of course, we can also prove this using the fact that the electric field at a point near an "infinite" sheet of charge is E = σ/[2ε0].
(a) LEFT OF THE PLATES: E = (σ/[2ε0])(-i) (from the right plate) + (σ/[2ε0])(i) (from the left plate) = 0
(b) RIGHT OF THE PLATES: E = (σ/[2ε0])(i) (from the right plate) + (σ/[2ε0])(-i) (from the left plate) = 0
(c) Between the plates, our field components will add, rather than cancel each other out.
E = (σ/[2ε0])(-i) + (σ/[2ε0])(-i) = (σ/ε0)(-i) = -[(7.00 x 10-22 C/m2)/(8.85 x 10-12 C2/N•m2)]i = -(7.91 x 10-11 N/C)i
Of course, we can also prove this using the fact that the electric field at a point near an "infinite" sheet of charge is E = σ/[2ε0].
(a) LEFT OF THE PLATES: E = (σ/[2ε0])(-i) (from the right plate) + (σ/[2ε0])(i) (from the left plate) = 0
(b) RIGHT OF THE PLATES: E = (σ/[2ε0])(i) (from the right plate) + (σ/[2ε0])(-i) (from the left plate) = 0
(c) Between the plates, our field components will add, rather than cancel each other out.
E = (σ/[2ε0])(-i) + (σ/[2ε0])(-i) = (σ/ε0)(-i) = -[(7.00 x 10-22 C/m2)/(8.85 x 10-12 C2/N•m2)]i = -(7.91 x 10-11 N/C)i
FINAL ANSWERS: (a) 0
(b) 0
(c) -(7.91 x 10-11 N/C)i
(b) 0
(c) -(7.91 x 10-11 N/C)i
•34. In Fig. 23-45, a small circular hole of radius R = 1.80 cm has been cut in the middle of an infinite, flat, nonconducting surface that has uniform charge density σ = 4.50 pC/m2.
A z axis, with its origin at the hole’s center, is perpendicular to the surface. In unit-vector notation, what is the electric field at point P at z = 2.56 cm? (Hint: See Eq. 22-26 and use superposition.)
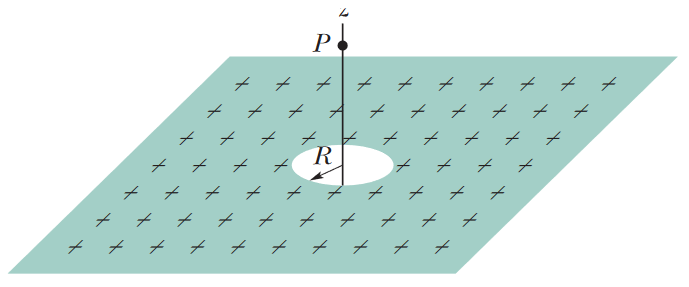

A: The formula for the electric field at a point near an "infinite" sheet of uniform charge is E1 = σ/[2ε0]. However, that alone won't perfectly reflect this situation, because there is
a circular "disk" of charge that is absent (where the hole is). We know that the formula for the electric field at a point coaxial with a disk of uniform charge is
E2 = σ/(2ε0) * (1 - z/sqrt[z2 + R2]). Since the point P is coaxial with the center of the hole (just as this formula requires), this formula for E2
represents the amount of field that is being lost due to the hole. With this, we can take the amount of field that would be produced at point P due to the disk and subtract it from the amount of field that
would be present due to the sheet on its own.
In order to keep this process in unit-vector notation, let's take E2 to be a vector with a negative surface charge density and use the superposition principle for electric fields to find a new formula that way.
E = E1 + E2 = (σ/[2ε0])(k) + (-σ)/(2ε0) * (1 - z/sqrt[z2 + R2]) * (k) = σz/(2ε0*sqrt[z2 + R2]) * (k) = (0.208 N/C)k
In order to keep this process in unit-vector notation, let's take E2 to be a vector with a negative surface charge density and use the superposition principle for electric fields to find a new formula that way.
E = E1 + E2 = (σ/[2ε0])(k) + (-σ)/(2ε0) * (1 - z/sqrt[z2 + R2]) * (k) = σz/(2ε0*sqrt[z2 + R2]) * (k) = (0.208 N/C)k
FINAL ANSWER: (0.208 N/C)k
•35. Figure 23-46a shows three plastic sheets that are large, parallel, and uniformly charged. Figure 23-46b gives the component of the net electric field along an x axis through the sheets.
The scale of the vertical axis is set by Es = 6.0 x 105 N/C. What is the ratio of the charge density on sheet 3 to that on sheet 2?
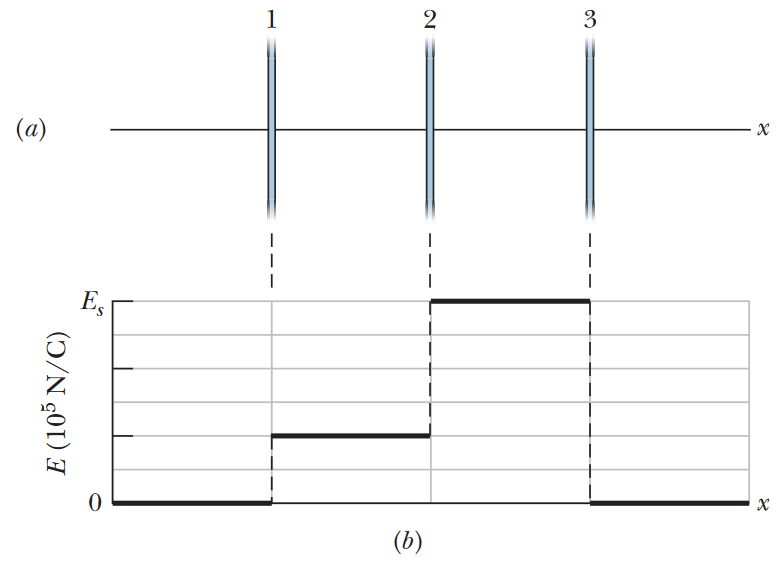

A: Based on the way the graph is aligned with the sheets, we can infer that sheets 1 and 2 are positively charged, and sheet 3 has a negative charge. We can also infer that the magnitude of charge
on sheet 3 is equal to the sum of the charges on sheets 1 and 2 (hence the fact that there is zero electric field outside the rings; the field from the positive charges must all terminate at whatever negative charges are
present). We can use the direction of the electric fields in each region of the system to set up a system of equations based on the fields given in the graph.
In the region between sheets 1 and 2: E1 - E2 + E3 = 2.0 x 105 N/C
In the region between sheets 2 and 3: E1 + E2 + E3 = 6.0 x 105 N/C
To the right of sheet 3 (outside the system): E1 + E2 - E3 = 0 --> E1 + E2 = E3
Solving this system of equations, we find that the magnitudes of the fields are E1 = 1.0 x 105 N/C, E2 = 2.0 x 105 N/C, and E3 = 3.0 x 105 N/C. Because the formula for electric field at a point near an infinite sheet of uniform charge is E = σ/(2ε0), we can see that the electric field is proportional to the surface charge density. From this, we can find the ratio of the magnitudes of the electric fields to get the ratio of the charge densities.
E3/E2 = [|σ3|/(2ε0)]/[|σ2|/(2ε0)] = |σ3|/|σ2| = (3.0 x 105 N/C)/(2.0 x 105 N/C) = 1.5
Of course, we still need to account for the signs of the charge densities. As we said earlier, the charge on sheet 3 is negative, and should therefore have a negative surface charge density. Since the surface charge density on sheet 2 is positive, this ratio should actually be negative.
In the region between sheets 1 and 2: E1 - E2 + E3 = 2.0 x 105 N/C
In the region between sheets 2 and 3: E1 + E2 + E3 = 6.0 x 105 N/C
To the right of sheet 3 (outside the system): E1 + E2 - E3 = 0 --> E1 + E2 = E3
Solving this system of equations, we find that the magnitudes of the fields are E1 = 1.0 x 105 N/C, E2 = 2.0 x 105 N/C, and E3 = 3.0 x 105 N/C. Because the formula for electric field at a point near an infinite sheet of uniform charge is E = σ/(2ε0), we can see that the electric field is proportional to the surface charge density. From this, we can find the ratio of the magnitudes of the electric fields to get the ratio of the charge densities.
E3/E2 = [|σ3|/(2ε0)]/[|σ2|/(2ε0)] = |σ3|/|σ2| = (3.0 x 105 N/C)/(2.0 x 105 N/C) = 1.5
Of course, we still need to account for the signs of the charge densities. As we said earlier, the charge on sheet 3 is negative, and should therefore have a negative surface charge density. Since the surface charge density on sheet 2 is positive, this ratio should actually be negative.
FINAL ANSWER: -1.5
•36. Figure 23-47 shows cross sections through two large, parallel, nonconducting sheets with identical distributions of positive charge with surface charge density
σ = 1.77 x 1022 C/m2. In unit-vector notation, what is E at points (a) above the sheets, (b) between them, and (c) below them?
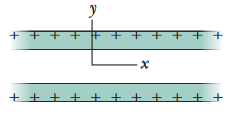

A: (a) The formula for the electric field at a point near an infinite sheet of uniform charge is E = σ/(2ε0). Notice that this formula is completely independent of the actual distance between
the sheet and the point being analyzed. Recall that electric field points away from positive charges, so in the region above both sheets, an electric field pointing "upwards" is coming from both sheets. Because
the surface charge densities of both sheets are equal, the total electric field at the point is
Etotal = σ/(2ε0) + σ/(2ε0) = σ/ε0 = (1.77 x 1022 C/m2)/(8.85 x 10-12 C2/N•m2) = 2.00 x 10-11 N/C
Of course, this is just a magnitude. Since the field is pointed away from the positive charges (and thus, it is pointed upwards in the region above both sheets), the vector should be written with the positive unit vector j: E = (2.00 x 10-11 N/C)j.
(b) Between both sheets, the electric field due to both sheets are pointing in the opposite direction. They will completely cancel each other out.
(c) Same logic as part (a), except now the field will be pointing downwards (away from the sheets), so we write the answer in the negative y direction instead: E = -(2.00 x 10-11 N/C)j
Etotal = σ/(2ε0) + σ/(2ε0) = σ/ε0 = (1.77 x 1022 C/m2)/(8.85 x 10-12 C2/N•m2) = 2.00 x 10-11 N/C
Of course, this is just a magnitude. Since the field is pointed away from the positive charges (and thus, it is pointed upwards in the region above both sheets), the vector should be written with the positive unit vector j: E = (2.00 x 10-11 N/C)j.
(b) Between both sheets, the electric field due to both sheets are pointing in the opposite direction. They will completely cancel each other out.
(c) Same logic as part (a), except now the field will be pointing downwards (away from the sheets), so we write the answer in the negative y direction instead: E = -(2.00 x 10-11 N/C)j
FINAL ANSWERS: (a) (2.00 x 10-11 N/C)j
(b) 0
(c) -(2.00 x 10-11 N/C)j
(b) 0
(c) -(2.00 x 10-11 N/C)j
•37. A square metal plate of edge length 8.0 cm and negligible thickness has a total charge of 6.0 x 106 C. (a) Estimate the magnitude E of the electric field just
off the center of the plate (at, say, a distance of 0.50 mm from the center) by assuming that the charge is spread uniformly over the two faces of the plate. (b) Estimate E at a distance of 30 m
(large relative to the plate size) by assuming that the plate is a charged particle.
A: Part (a) of this problem is actually somewhat of a trick question. Your first instinct might be to apply the formula for the electric field at a point near an infinite sheet of charge
[σ/(2ε0)], but it's important to always keep in mind how every formula you use was derived; when this formula was derived, it was specifically in reference to a single sheet of uniform charge,
without regard for the fact that a plate or thin object technically has two faces. This problem also says that the plate has "negligible thickness", but the problem is still careful to specify that the charge is spread over
"the two faces of the plate". This changes the situation somewhat, and we'll need to rethink the formula we use.
Let's apply Gauss' law and derive our own formula to use here. Using the cylinder derivation described in the chapter, we can represent the flux through each side of the cylinder.
ε0∮E•dA = qenc
ε0(EA + EA) = qenc
ε0(2EA) = qenc
This is pretty much identical to the original derivation, so far. The next step is to replace qenc with a formula that represents the amount of enclosed charge in terms of the surface charge density. With a single sheet of charge, this is represented by qenc = σA, where A is the surface area on one face of the plate. However, since we have a plate with an equal amount of charge density spread through both sides of the plate, we should multiply this by 2. Our Gauss' law derivation can now proceed.
ε0(2EA) = 2σA
ε0E = σ --> E = σ/ε0
This is the actual formula we'll be using for the field. We now just need to find the surface charge density on the plate, so that we can actually use this formula. Since the charge is uniformly distributed over both sides of the plate, the surface charge density on the plate is σ = q/(2A).
σ = q/(2A) = (6.0 x 10-6 C)/[2(0.80 m)2] = 4.69 x 10-4 C/m2
E = σ/ε0 = (4.69 x 10-4 C/m2)/(8.85 x 10-12 C2/N•m2) = 5.3 x 107 N/C
(b) The formula for the electric field at some radial distance from a point charge is E = kq/r2, where q is the total charge on the plate, and r is the distance between the charge and the point being analyzed.
E = kq/r2 = (8.99 x 109 N•m2/C2)(6.0 x 106 C)/(30 m)2 = 60 N/C
Let's apply Gauss' law and derive our own formula to use here. Using the cylinder derivation described in the chapter, we can represent the flux through each side of the cylinder.
ε0∮E•dA = qenc
ε0(EA + EA) = qenc
ε0(2EA) = qenc
This is pretty much identical to the original derivation, so far. The next step is to replace qenc with a formula that represents the amount of enclosed charge in terms of the surface charge density. With a single sheet of charge, this is represented by qenc = σA, where A is the surface area on one face of the plate. However, since we have a plate with an equal amount of charge density spread through both sides of the plate, we should multiply this by 2. Our Gauss' law derivation can now proceed.
ε0(2EA) = 2σA
ε0E = σ --> E = σ/ε0
This is the actual formula we'll be using for the field. We now just need to find the surface charge density on the plate, so that we can actually use this formula. Since the charge is uniformly distributed over both sides of the plate, the surface charge density on the plate is σ = q/(2A).
σ = q/(2A) = (6.0 x 10-6 C)/[2(0.80 m)2] = 4.69 x 10-4 C/m2
E = σ/ε0 = (4.69 x 10-4 C/m2)/(8.85 x 10-12 C2/N•m2) = 5.3 x 107 N/C
(b) The formula for the electric field at some radial distance from a point charge is E = kq/r2, where q is the total charge on the plate, and r is the distance between the charge and the point being analyzed.
E = kq/r2 = (8.99 x 109 N•m2/C2)(6.0 x 106 C)/(30 m)2 = 60 N/C
FINAL ANSWERS: (a) 5.3 x 107 N/C
(b) 60 N/C
(b) 60 N/C
Applying Gauss' Law: Spherical Symmetry
•44. Figure 23-52 gives the magnitude of the electric field inside and outside a sphere with a positive charge distributed uniformly throughout its volume. The scale of the vertical axis
is set by Es = 5.0 x 107 N/C. What is the charge on the sphere?
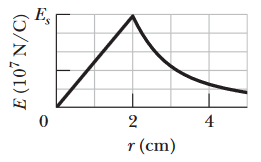

A: Let's analyze the graph to determine what exactly is happening here. From 0 ≤ r ≤ 2 cm, the relationship between E and r is linear. This lines up with E = (q/[4πε0R3])*r,
where r is the radius of the Gaussian surface and R is the radius of the total amount of charge present. This is the formula that applies when the Gaussian sphere is smaller than the sphere of charge.
After this, the function starts sloping downwards in what looks like an inverse-squared relationship. This aligns with the formula for the electric field due to a uniformly charged sphere, E = q/(4πε0r2).
From all of this, we can infer that the point on the graph with the maximum electric field (r = 2 cm) is the point at which the G-sphere has enclosed all of the charge in the sphere. We can use this to find the q from the formula for electric field at a distance from a point charge. Solve for q:
E = q/(4πε0r2) = kq/r2 --> q = r2E/k = (0.020 m)2(5.0 x 107 N/C)/(8.99 x 109 N•m2/C2) = 2.2 x 10-6 C
After this, the function starts sloping downwards in what looks like an inverse-squared relationship. This aligns with the formula for the electric field due to a uniformly charged sphere, E = q/(4πε0r2).
From all of this, we can infer that the point on the graph with the maximum electric field (r = 2 cm) is the point at which the G-sphere has enclosed all of the charge in the sphere. We can use this to find the q from the formula for electric field at a distance from a point charge. Solve for q:
E = q/(4πε0r2) = kq/r2 --> q = r2E/k = (0.020 m)2(5.0 x 107 N/C)/(8.99 x 109 N•m2/C2) = 2.2 x 10-6 C
FINAL ANSWER: 2.2 x 10-6 C
•45. Two charged concentric spherical shells have radii 10.0 cm and 15.0 cm. The charge on the inner shell is 4.00 x 108 C, and that on the outer shell is 2.00 x 10-8 C.
Find the electric field (a) at r = 12.0 cm and (b) at r = 20.0 cm.
A: (a) At r = 12.0 cm, the Gaussian sphere we can set up with that radius will enclose the inner shell, but not the outer shell. We can use our electric field formula to solve for the electric field there
based on the charge from shell 1.
E = q1/(4πε0r2) = (8.99 x 109 N•m2/C2)(4.00 x 108 C)/(0.120 m)2 = 2.50 x 104 N/C
(b) At r = 20.0 cm, the G-sphere surrounds both shells, so we want to relate the field there to the sum of the charges from both shells.
E = (q1 + q2)/(4πε0r2) = (8.99 x 109 N•m2/C2)(4.00 + 2.00)(10-8)/(0.200 m)2 = 1.35 x 104 N/C
E = q1/(4πε0r2) = (8.99 x 109 N•m2/C2)(4.00 x 108 C)/(0.120 m)2 = 2.50 x 104 N/C
(b) At r = 20.0 cm, the G-sphere surrounds both shells, so we want to relate the field there to the sum of the charges from both shells.
E = (q1 + q2)/(4πε0r2) = (8.99 x 109 N•m2/C2)(4.00 + 2.00)(10-8)/(0.200 m)2 = 1.35 x 104 N/C
FINAL ANSWERS: (a) 2.50 x 104 N/C
(b) 1.35 x 104 N/C
(b) 1.35 x 104 N/C
•46. Assume that a ball of charged particles has a uniformly distributed negative charge density except for a narrow radial tunnel through its center, from the surface on
one side to the surface on the opposite side. Also assume that we can position a proton anywhere along the tunnel or outside the ball. Let FR be the magnitude of the electrostatic force on the
proton when it is located at the ball’s surface, at radius R. As a multiple of R, how far from the surface is there a point where the force magnitude is 0.50FR if we move the proton (a) away from the ball and
(b) into the tunnel?
A: (a) The electrostatic force at some point outside the ball (based on both Coulomb's law and electric field formulas proven by Gauss' law) is F = qe/(4πε0r2).
For the electrostatic force specifically on the surface of the ball, this formula is FR = qe/(4πε0R2), where R is the radius of the ball, and we use "e" (the elementary charge)
for one of the charges because we're dealing with protons here. We solve this formula so that the force magnitude on the proton is half of FR, and solve for r.
F = 1/2 * FR
qe/(4πε0r2) = 1/2 * qe/(4πε0R2)
1/(r2) = 1/2 * 1/(R2)
2R2 = r2
r = sqrt(2) * R = 0.41R
(b) This time, we're looking for a location for the proton inside the ball. Once again, if we imagine some Gaussian surface within the charge, not enclosing the entire ball, it becomes clear that we should use the formula for a uniform charge field when r ≤ R; Einside = qr/(4πε0R3). The formula for the force due to this field can be found by multiplying the proton's charge. We can then apply a similar process to that of part (a).
Finside = qre/(4πε0R3)
Finside = 1/2 * FR
qre/(4πε0R3) = 1/2 * qe/(4πε0R2)
r/(R) = 1/2
r = R/2 = 0.50R
F = 1/2 * FR
qe/(4πε0r2) = 1/2 * qe/(4πε0R2)
1/(r2) = 1/2 * 1/(R2)
2R2 = r2
r = sqrt(2) * R = 0.41R
(b) This time, we're looking for a location for the proton inside the ball. Once again, if we imagine some Gaussian surface within the charge, not enclosing the entire ball, it becomes clear that we should use the formula for a uniform charge field when r ≤ R; Einside = qr/(4πε0R3). The formula for the force due to this field can be found by multiplying the proton's charge. We can then apply a similar process to that of part (a).
Finside = qre/(4πε0R3)
Finside = 1/2 * FR
qre/(4πε0R3) = 1/2 * qe/(4πε0R2)
r/(R) = 1/2
r = R/2 = 0.50R
FINAL ANSWERS: (a) 0.41R
(b) 0.50R
(b) 0.50R
•47. An unknown charge sits on a conducting solid sphere of radius 10 cm. If the electric field 15 cm from the center of the sphere has the magnitude 3.0 x 103 N/C
and is directed radially inward, what is the net charge on the sphere?
A: The charge is uniformly distributed over the surface of the sphere. As Gauss' law has proven, this is essentially equal to if all the charge was concentrated at a single point. The magnitude of the
electric field created by this charge is then E = |q|/(4πε0r2). The charge can then be found:
|q| = 4πε0r2E = (0.15 m)2(3.0 x 103 N/C)/(8.99 x 109 N•m2/C2) = 7.5 x 10-9 C = 7.5 nC
The problem specifies that the field is directed radially inward. Because electric fields point toward negative charges, we can say that the charge on the surface of the sphere is negative.
|q| = 4πε0r2E = (0.15 m)2(3.0 x 103 N/C)/(8.99 x 109 N•m2/C2) = 7.5 x 10-9 C = 7.5 nC
The problem specifies that the field is directed radially inward. Because electric fields point toward negative charges, we can say that the charge on the surface of the sphere is negative.
FINAL ANSWER: -7.5 nC