This chapter covers electric fields, electric field lines, electric dipoles, and point charges within electric fields.
If you would like me to go over a certain problem, or contact me for any other reason, please email me at kevinbarbuto@gmail.com. If you want to support my work and help me continue to maintain sites like this, subscribe to my YouTube channel here.
Part 1: Chapter 22 Conceptual Questions and Problems
ProblemsThe Electric Field
•1. Sketch qualitatively the electric field lines both between and outside two concentric conducting spherical shells when a uniform
positive charge q1 is on the inner shell and a uniform negative charge -q2 is on the outer.
Consider the cases q1 > q2, q1 = q2, and q1 < q2.
A: Remember the rules and conventions for constructing electric field lines. Specifically, electric field lines are generally drawn so that
they originate at positive charges and terminate at negative charges. The "closeness" or "density" of the electric field lines is also intended to be proportional
to the magnitude of the field at any point. If a certain amount of positive charge originates from the inner shell, and an equal negative charge is on the outer shell,
then the entire field should dissipate once it reaches the outer shell. The case where q1 = q2 should then be drawn as follows:
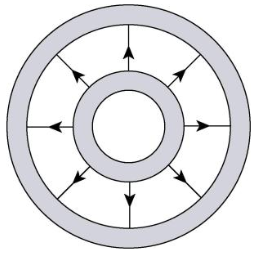
If q1 > q2, however, then there will be "more" electric field coming from the inner shell, and not all of it terminates at the outer shell. We can show this by drawing additional field lines extending beyond the outer shell.
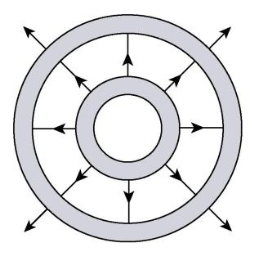
Since some of the electric field lines are still terminating at the outer shell, of course, we draw the "outer" field lines as fewer and farther apart than they are between the shells. We use a similar line of logic in constructing the field lines where q1 < q2. All of the field lines from the inner shell will terminate at the outer shell, but there still remains some "room" for more field lines to terminate there. We'll draw some field lines pointing to the outer shell, originating from outside the system:
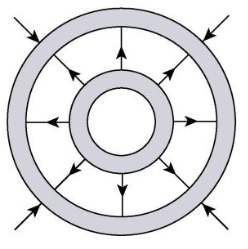

If q1 > q2, however, then there will be "more" electric field coming from the inner shell, and not all of it terminates at the outer shell. We can show this by drawing additional field lines extending beyond the outer shell.

Since some of the electric field lines are still terminating at the outer shell, of course, we draw the "outer" field lines as fewer and farther apart than they are between the shells. We use a similar line of logic in constructing the field lines where q1 < q2. All of the field lines from the inner shell will terminate at the outer shell, but there still remains some "room" for more field lines to terminate there. We'll draw some field lines pointing to the outer shell, originating from outside the system:

FINAL ANSWERS: (see the above diagrams)
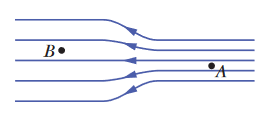
•2. In Fig. 22-34 the electric field lines on the left have twice the separation of those on the right.
(a) If the magnitude of the field at A is 40 N/C, what is the magnitude of the force on a proton at A? (b) What is the magnitude of the field at B?

A: (a) The electric field of a charge at a specific point is given by E = F/q0.
Solving for force gives us F = q0E. If we assume that the diagram follows an x axis coordinate system, then the electric field should be negative,
because it can be seen pointing to the left. We can use this fact, and the knowledge that the charge on a proton is +1.6 x 10-19 C, to solve for force:
F = (+1.6 x 10-19 C)(-40 N/C i) = (-6.4 x 10-18 N)i
Of course, we're only asked to give the magnitude anyway, so we would give our answer as 6.4 x 10-18 N (but with the understanding that the field vector points leftward, -i).
(b) Recall that the "strength" of an electric field is intended to be proportional to the density of the electric field lines. If the field lines at point B have "twice the separation" of the field lines at point A, then the electric field at point B will be half as strong as that of the field at point A.
EB = EA/2 = (40 N/C)/2 = 20 N/C.
F = (+1.6 x 10-19 C)(-40 N/C i) = (-6.4 x 10-18 N)i
Of course, we're only asked to give the magnitude anyway, so we would give our answer as 6.4 x 10-18 N (but with the understanding that the field vector points leftward, -i).
(b) Recall that the "strength" of an electric field is intended to be proportional to the density of the electric field lines. If the field lines at point B have "twice the separation" of the field lines at point A, then the electric field at point B will be half as strong as that of the field at point A.
EB = EA/2 = (40 N/C)/2 = 20 N/C.
FINAL ANSWERS: (a) 6.4 x 10-18 N
(b) 20 N/C
(b) 20 N/C
The Electric Field Due to a Charged Particle
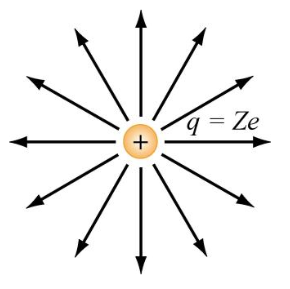
•3. The nucleus of a plutonium-239 atom contains 94 protons. Assume that the nucleus is a sphere with radius 6.64 fm and
with the charge of the protons uniformly spread through the sphere. At the surface of the nucleus, what are the (a) magnitude and
(b) direction (radially inward or outward) of the electric field produced by the protons?
A: The formula for the electric field due to a charged particle q is E = q/(4πε0R2). In this case, our charge q is equal to the
combined charge of 94 protons, so we can say that q = 94e, where "e" refers to the elementary charge (the charge of one proton). It's also useful to realize that
the a sphere with a charge that is uniformly distributed on the surface will have the same electric field as though the charges were all at the center of the nucleus,
so we can just use the radius of the sphere for R.
E = 94e/(4πε0R2) = (8.99 x 109 N•m2/C2)(94)(1.6 x 10-19 C)/(6.64 x 10-15 m)2 = 3.07 x 1021 N/C.
(b) Electric field lines conventionally point out from positive charges and into negative charges. Because this nucleus' charge comes from protons (which are positively charged), the electric field lines will point radially outward from the sphere.
E = 94e/(4πε0R2) = (8.99 x 109 N•m2/C2)(94)(1.6 x 10-19 C)/(6.64 x 10-15 m)2 = 3.07 x 1021 N/C.
(b) Electric field lines conventionally point out from positive charges and into negative charges. Because this nucleus' charge comes from protons (which are positively charged), the electric field lines will point radially outward from the sphere.

(In this diagram, Z represents the number of protons in the charge.)
FINAL ANSWERS: (a) 3.07 x 1021 N/C
(b) Outward
(b) Outward
•4. Two charged particles are attached to an x axis: Particle 1 of charge -2.00 x 10-7 C is at position x = 6.00 cm and particle 2 of charge +2.00 x 10-7 C is at
position x = 21.0 cm. Midway between the particles, what is their net electric field in unit-vector notation?
A: At some midpoint between the particles, the net electric field will be the sum of the electric fields from both particles (as per the principle of superposition). Let's first figure out what the midpoint
actually is, by taking the average of the position values we're given:
x = (x1 + x2)/2 = (6.00 cm + 21.00 cm)/2 = 13.5 cm
The magnitude for the electric field due to a particle is given by E = |q|/(4πε0r2), where r is the distance between the particle creating the field and the particle being affected by the field. We also take into account the direction of each field. Recall that field lines are directed from a positive charge to a negative charge, so the field will be leaving particle 2 and terminating at particle 1. Because particle 2 is positioned "to the right" of particle 1 (assuming we're working on an x axis here), then both electric fields in this problem are directed to the left, in the negative x direction. When we write the formulas for the fields, we note the fact that both fields must be negative.
E1 = - |q1|/(4πε0(x - x1)2) * (i) = - (8.99 x 109 N•m2/C2)(2.00 x 10-7 C)/(0.135 m - 0.060 m)2 * (i) = -(3.196 x 105 N/C) i
E2 = - |q2|/(4πε0(x - x2)2) * (i) = - (8.99 x 109 N•m2/C2)(2.00 x 10-7 C)/(0.135 m - 0.210 m)2 * (i) = -(3.196 x 105 N/C) i
Of course, because electric fields obey the principle of superposition, the net electric field at point x will be the sum of both components:
Enet = E1 + E2 = -(6.39 x 105 N/C)i
x = (x1 + x2)/2 = (6.00 cm + 21.00 cm)/2 = 13.5 cm
The magnitude for the electric field due to a particle is given by E = |q|/(4πε0r2), where r is the distance between the particle creating the field and the particle being affected by the field. We also take into account the direction of each field. Recall that field lines are directed from a positive charge to a negative charge, so the field will be leaving particle 2 and terminating at particle 1. Because particle 2 is positioned "to the right" of particle 1 (assuming we're working on an x axis here), then both electric fields in this problem are directed to the left, in the negative x direction. When we write the formulas for the fields, we note the fact that both fields must be negative.
E1 = - |q1|/(4πε0(x - x1)2) * (i) = - (8.99 x 109 N•m2/C2)(2.00 x 10-7 C)/(0.135 m - 0.060 m)2 * (i) = -(3.196 x 105 N/C) i
E2 = - |q2|/(4πε0(x - x2)2) * (i) = - (8.99 x 109 N•m2/C2)(2.00 x 10-7 C)/(0.135 m - 0.210 m)2 * (i) = -(3.196 x 105 N/C) i
Of course, because electric fields obey the principle of superposition, the net electric field at point x will be the sum of both components:
Enet = E1 + E2 = -(6.39 x 105 N/C)i
FINAL ANSWER: -(6.39 x 105 N/C)i
•5. A charged particle produces an electric field with a magnitude of 2.0 N/C at a point that is 50 cm away from the particle. What is the magnitude of the particle’s charge?
A: The magnitude of the electric field due to a charged particle is E = |q|/(4πε0r2). Solve for |q|:
E = |q|/(4πε0r2) --> |q| = 4πε0r2E = (0.50 m)2(2.0 N/C)/(8.99 x 109 N•m2/C2) = 5.6 x 10-11 C
E = |q|/(4πε0r2) --> |q| = 4πε0r2E = (0.50 m)2(2.0 N/C)/(8.99 x 109 N•m2/C2) = 5.6 x 10-11 C
FINAL ANSWER: 5.6 x 10-11 C
•6. What is the magnitude of a point charge that would create an electric field of 1.00 N/C at points 1.00 m away?
A: The magnitude of the electric field due to a charged particle is E = |q|/(4πε0r2). Solve for |q|:
E = |q|/(4πε0r2) --> |q| = 4πε0r2E = (1.00 m)2(1.00 N/C)/(8.99 x 109 N•m2/C2) = 1.11 x 10-10 C
E = |q|/(4πε0r2) --> |q| = 4πε0r2E = (1.00 m)2(1.00 N/C)/(8.99 x 109 N•m2/C2) = 1.11 x 10-10 C
FINAL ANSWER: 1.11 x 10-10 C
The Electric Field Due to a Dipole
The Electric Field Due to a Line of Charge
•22. Density, density, density. (a) A charge -300e is uniformly distributed along a circular arc of radius 4.00 cm, which subtends an angle of 40°. What is the linear charge density along the arc?
(b) A charge -300e is uniformly distributed over one face of a circular disk of radius 2.00 cm. What is the surface charge density over that face? (c) A charge -300e is uniformly distributed over the surface
of a sphere of radius 2.00 cm. What is the surface charge density over that surface? (d) A charge -300e is uniformly spread through the volume of a sphere of radius 2.00 cm. What is the volume
charge density in that sphere?
A: (a) A linear charge density refers to the amount of charge per unit of length, within an approximate "line" of charge. Reasonably, a linear charge density λ is written as λ = q/L. We're given the
charge by the problem, but not the length of the line of charge. However, we should know that the length of a circular arc is found by L = rθ, where r is the radius of the arc, and θ is the angle of the arc. Let's find the length,
but note that this formula only works if θ is in radians.
L = (.0400 m)(40°)(π/180) = 0.0279 m
Now we can solve for λ (and remember that e is the elementary charge).
λ = -300(1.602 x 10-19 C)/(0.0279 m) = -1.72 x 10-15 C/m
(b) This time we're looking for the surface charge density over the area of a disk. The area of the disk is A = πr2 = π(0.0200 m)2. The surface charge density is then
σ = q/Acircle = -300(1.602 x 10-19 C)/[π(0.0200 m)2] = -3.82 x 10-14 C/m2
(c) We're still looking for a surface charge density, but this time on a sphere. The surface area of a sphere is A = 4πr2.
σ = q/Asphere = -300(1.602 x 10-19 C)/[4π(0.0200 m)2] = -9.56 x 10-15 C/m2
(d) Now we want a volume charge density throughout a sphere. The volume of a sphere is V = 4πr3/3.
ρ = q/V = -300(1.602 x 10-19 C)/[4π(0.0200 m)3/3] = -1.43 x 10-12 C/m3
L = (.0400 m)(40°)(π/180) = 0.0279 m
Now we can solve for λ (and remember that e is the elementary charge).
λ = -300(1.602 x 10-19 C)/(0.0279 m) = -1.72 x 10-15 C/m
(b) This time we're looking for the surface charge density over the area of a disk. The area of the disk is A = πr2 = π(0.0200 m)2. The surface charge density is then
σ = q/Acircle = -300(1.602 x 10-19 C)/[π(0.0200 m)2] = -3.82 x 10-14 C/m2
(c) We're still looking for a surface charge density, but this time on a sphere. The surface area of a sphere is A = 4πr2.
σ = q/Asphere = -300(1.602 x 10-19 C)/[4π(0.0200 m)2] = -9.56 x 10-15 C/m2
(d) Now we want a volume charge density throughout a sphere. The volume of a sphere is V = 4πr3/3.
ρ = q/V = -300(1.602 x 10-19 C)/[4π(0.0200 m)3/3] = -1.43 x 10-12 C/m3
FINAL ANSWERS: (a) -1.72 x 10-15 C/m
(b) -3.82 x 10-14 C/m2
(c) -9.56 x 10-15 C/m2
(d) -1.43 x 10-12 C/m3
(b) -3.82 x 10-14 C/m2
(c) -9.56 x 10-15 C/m2
(d) -1.43 x 10-12 C/m3
•23. Figure 22-47 shows two parallel nonconducting rings with their central axes along a common line. Ring 1 has uniform charge
q1 and radius R; ring 2 has uniform charge
q2 and the same radius R. The rings are separated by distance d = 3.00R. The net electric field at point P on the common line, at distance R from ring 1, is zero.
What is the ratio q1/q2?
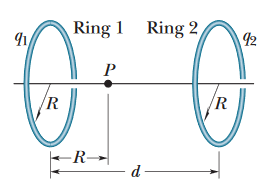

A: As derived in the textbook chapter, the formula for the electric field at a point on the axis of a circular line of charge is E = qz/[4πε0(z2 + R2)3/2].
In this equation, R is the radius of the circle of charge, and z is the distance between the center of the circle and the point we're analyzing.
At the electric field at point P due to the left ring, z = R, since the radius of the ring is also the distance between the left ring and point P. This tells us that Eleft ring = q1R/[4πε0(R2 + R2)3/2]. The problem tells us that the distance between both circles, d, is three times R, so the distance between the right ring and point P is 2R. This means that Eright ring = q2(2R)/[4πε0[(2R)2 + R2]3/2].
The problem tells us that the net electric field at point P is zero, meaning that the electric fields from each ring must have equal magnitudes at point P in order to cancel each other out. We can solve for the ratio:
Eleft ring = Eright ring
q1R/[4πε0(R2 + R2)3/2] = q2(2R)/[4πε0[(2R)2 + R2]3/2]
q1/[(2R2)3/2] = 2q2/[(5R2)3/2]
--> q1/q2 = 2(2/5)3/2 ≈ 0.506
At the electric field at point P due to the left ring, z = R, since the radius of the ring is also the distance between the left ring and point P. This tells us that Eleft ring = q1R/[4πε0(R2 + R2)3/2]. The problem tells us that the distance between both circles, d, is three times R, so the distance between the right ring and point P is 2R. This means that Eright ring = q2(2R)/[4πε0[(2R)2 + R2]3/2].
The problem tells us that the net electric field at point P is zero, meaning that the electric fields from each ring must have equal magnitudes at point P in order to cancel each other out. We can solve for the ratio:
Eleft ring = Eright ring
q1R/[4πε0(R2 + R2)3/2] = q2(2R)/[4πε0[(2R)2 + R2]3/2]
q1/[(2R2)3/2] = 2q2/[(5R2)3/2]
--> q1/q2 = 2(2/5)3/2 ≈ 0.506
FINAL ANSWER: 0.506
The Electric Field Due to a Charged Disk
•34. A disk of radius 2.5 cm has a surface charge density of 5.3 μC/m2 on its upper face. What is the magnitude of the electric field produced by the disk at a point
on its central axis at distance z = 12 cm from the disk?
A: The formula for the electric field at a point coaxial with a uniformly charged disk is E = σ/(2ε0) * (1 - z/sqrt[z2 + R2]). The distance between the center of the disk
and the point on the axis is z, R is the radius of the disk, and σ is the surface charge density of the disk. Fortunately for us, all three of these variables are given to us by the problem.
E = σ/(2ε0) * (1 - z/sqrt[z2 + R2]) = (5.3 x 10-6 C/m2)/(2ε0) * (1 - [12 cm]/sqrt[(12 cm)2 + (2.5 cm)2]) = 6.3 x 103 N/C
I didn't bother converting from centimeters to meters in this case, because those units cancel out before they even interact with the other values in the equation. Understanding dimensional analysis is quite handy in minimizing work sometimes!
E = σ/(2ε0) * (1 - z/sqrt[z2 + R2]) = (5.3 x 10-6 C/m2)/(2ε0) * (1 - [12 cm]/sqrt[(12 cm)2 + (2.5 cm)2]) = 6.3 x 103 N/C
I didn't bother converting from centimeters to meters in this case, because those units cancel out before they even interact with the other values in the equation. Understanding dimensional analysis is quite handy in minimizing work sometimes!
FINAL ANSWER: 6.3 x 103 N/C
•35. At what distance along the central perpendicular axis of a uniformly charged plastic disk of radius 0.600 m is the magnitude of the electric field equal to one-half the magnitude of
the field at the center of the surface of the disk?
A: The formula for the electric field at a point coaxial with a uniformly charged disk is E = σ/(2ε0) * (1 - z/sqrt[z2 + R2]). When we look at a point on the center of the
surface of the disk (in other words, where z = 0), Ec = σ/(2ε0).
Let the magnitude of the electric field at the center of the surface of the disk be Ec. Let's also let the magnitude of the electric field some distance away from the disk, on its axis of symmetry, be E. We're looking for wherever E is equal to one half of Ec, or E = 1/2 * Ec. We can set this up as a ratio by writing it as E/Ec = 1/2. Let's try writing this ratio with our electric field formulas.
E/Ec = [σ/(2ε0) * (1 - z/sqrt[z2 + R2])] / [σ/(2ε0)] = 1 - z/sqrt[z2 + R2]
We've simplified the ratio as 1 - z/sqrt[z2 + R2]. Of course, this has to be equal to 1/2.
1 - z/sqrt[z2 + R2] = 1/2 --> z/sqrt[z2 + R2] = 1/2
Now let's solve for z.
(z/sqrt[z2 + R2])2 = (1/2)2
z2/(z2 + R2) = 1/4
z2 = (z2 + R2)/4
4z2 = z2 + R2
3z2 = R2
z2 = R2/3
z = R/sqrt(3) = (0.600 m)/sqrt(3) = 0.346 m
Let the magnitude of the electric field at the center of the surface of the disk be Ec. Let's also let the magnitude of the electric field some distance away from the disk, on its axis of symmetry, be E. We're looking for wherever E is equal to one half of Ec, or E = 1/2 * Ec. We can set this up as a ratio by writing it as E/Ec = 1/2. Let's try writing this ratio with our electric field formulas.
E/Ec = [σ/(2ε0) * (1 - z/sqrt[z2 + R2])] / [σ/(2ε0)] = 1 - z/sqrt[z2 + R2]
We've simplified the ratio as 1 - z/sqrt[z2 + R2]. Of course, this has to be equal to 1/2.
1 - z/sqrt[z2 + R2] = 1/2 --> z/sqrt[z2 + R2] = 1/2
Now let's solve for z.
(z/sqrt[z2 + R2])2 = (1/2)2
z2/(z2 + R2) = 1/4
z2 = (z2 + R2)/4
4z2 = z2 + R2
3z2 = R2
z2 = R2/3
z = R/sqrt(3) = (0.600 m)/sqrt(3) = 0.346 m
FINAL ANSWER: 0.346 m
A Point Charge in an Electric Field
•39. In Millikan’s experiment, an oil drop of radius 1.64 μm and density 0.851 g/cm3 is suspended in chamber C (Fig. 22-16) when a downward electric field of 1.92 x 105 N/C
is applied. Find the charge on the drop, in terms of e.
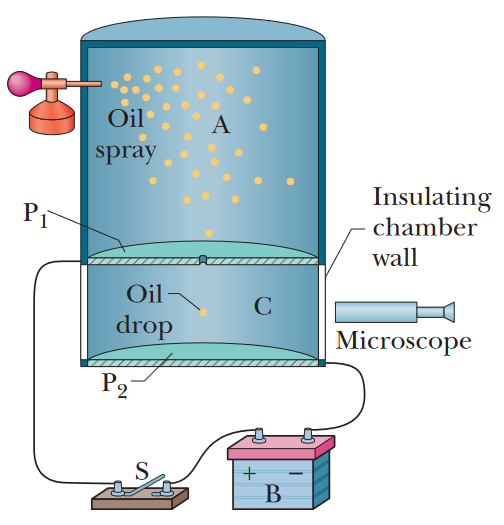

A: There are two forces acting on the oil drop. The force of gravity, acting downward, and the force due to the electric field, also acting downward. Both forces are pointed in the same direction (downwards).
Because the oil drop is "suspended" in the air, the combined effects of these forces must be zero. Let's use this information to write out a force equation, taking "downward" to be the positive direction.
Fg + Fe = 0
mg + qE = 0
We have substituted qE for the electric force, because that is one of the formulas for an electrostatic force due to an electric field. We have also substituted mg in for Fg, as that is the definition of weight.
It may seem odd that two forces pointing in the same direction should lead to the drop being suspended in air, but keep in mind that an electric field points in the direction that the affected particle will accelerate only if that particle is positively charged. Because an electric field points from a positive charge to a negative charge, any positive charge within the field will move along the direction of the field lines (the positive charges will repel it, and the negative charges will attract it). Any negative charge (such as that of an electron) will exhibit the opposite behavior; it will accelerate in the direction opposite to the direction of the electric field lines. Therefore, electric force on the particle is attempting to make it accelerate in the direction opposite to the direction of the force of gravity. Since the gravitational force and the electric force must be equal in magnitude and opposite in direction in order for the net force to be zero, we can write this as
mg = -qE
Solve for q.
q = -mg/E
We don't have the mass of the drop, but we can determine it by using the fact that mass is equal to volume times density (ρ = m/V --> m = Vρ), where the volume of the drop can be approximated as the volume of a sphere (V = 4πr3/3).
q = -mg/E = -4πr3ρg/[3E] = -4π(1.64 x 10-6 m)3(851 kg/m3)g/[3(1.92 x 105 N/C)] = -8.0 x 10-19 C
We want this charge in terms of e (the elementary charge), so let's divide this charge by e.
q/e = (-8.0 x 10-19 C)/(1.6 x 10-19 C) = -5
So the charge on the oil drop is q = -5e.
Fg + Fe = 0
mg + qE = 0
We have substituted qE for the electric force, because that is one of the formulas for an electrostatic force due to an electric field. We have also substituted mg in for Fg, as that is the definition of weight.
It may seem odd that two forces pointing in the same direction should lead to the drop being suspended in air, but keep in mind that an electric field points in the direction that the affected particle will accelerate only if that particle is positively charged. Because an electric field points from a positive charge to a negative charge, any positive charge within the field will move along the direction of the field lines (the positive charges will repel it, and the negative charges will attract it). Any negative charge (such as that of an electron) will exhibit the opposite behavior; it will accelerate in the direction opposite to the direction of the electric field lines. Therefore, electric force on the particle is attempting to make it accelerate in the direction opposite to the direction of the force of gravity. Since the gravitational force and the electric force must be equal in magnitude and opposite in direction in order for the net force to be zero, we can write this as
mg = -qE
Solve for q.
q = -mg/E
We don't have the mass of the drop, but we can determine it by using the fact that mass is equal to volume times density (ρ = m/V --> m = Vρ), where the volume of the drop can be approximated as the volume of a sphere (V = 4πr3/3).
q = -mg/E = -4πr3ρg/[3E] = -4π(1.64 x 10-6 m)3(851 kg/m3)g/[3(1.92 x 105 N/C)] = -8.0 x 10-19 C
We want this charge in terms of e (the elementary charge), so let's divide this charge by e.
q/e = (-8.0 x 10-19 C)/(1.6 x 10-19 C) = -5
So the charge on the oil drop is q = -5e.
FINAL ANSWER: -5e
•40. An electron with a speed of 5.00 x 108 cm/s enters an electric field of magnitude 1.00 x 103 N/C, traveling along a field line in the direction that retards its motion.
(a) How far will the electron travel in the field before stopping momentarily, and (b) how much time will have elapsed? (c) If the region containing the electric field is 8.00 mm long (too short for the electron to
stop within it), what fraction of the electron’s initial kinetic energy will be lost in that region?
A: (a) We can use the "v squared" kinematics formula for this. The acceleration of the electron, based on Newton's second law, is a = F/m = -eE/me. ... F is equal to qE in this case
(force due to an electric field), and the charge "q" is the charge on the electron, the elementary charge. It's written as negative in this case, because the electron's acceleration opposes the electric field vector.
v2 = v02 + 2ax --> x = [v2 - v02]/[2a] = -v02/[2a] = -v02/[2a] = -mev02/[-2eE] = -(9.11 x 10-31 kg)(5.00 x 106 m/s)2/[-2e(1.00 x 103 N/C)] = 7.12 x 10-2 m
(b) Now that we have the distance the electron travelled before it stopped, we can find the amount of time it took using the formula t = Δx/vavg.
t = Δx/vavg = 2Δx/vi = 2(7.12 x 10-2 m)/(5.00 x 106 m/s) = 2.85 x 10-8 s
(c) Let Ki be the initial kinetic energy, and solve with basic kinematics.
ΔK/Ki = Δ(1/2 * mev2)/(1/2 * mevi2) = Δv2/vi2 = 2aΔx/vi2 = -2eEΔx/[mevi2]
In this case, we use the new distance of the field given for Δx, 8.00 mm = 8.00 x 10-3 m.
ΔK/Ki= -2(1.60 x 10-19 C)(1.00 x 103 N/C)(8.00 x 10-3 m)/[(9.11 x 10-31 kg)(5.00 x 106 m/s)2] = -0.112
The fraction lost is then 0.112, or 11.2%.
v2 = v02 + 2ax --> x = [v2 - v02]/[2a] = -v02/[2a] = -v02/[2a] = -mev02/[-2eE] = -(9.11 x 10-31 kg)(5.00 x 106 m/s)2/[-2e(1.00 x 103 N/C)] = 7.12 x 10-2 m
(b) Now that we have the distance the electron travelled before it stopped, we can find the amount of time it took using the formula t = Δx/vavg.
t = Δx/vavg = 2Δx/vi = 2(7.12 x 10-2 m)/(5.00 x 106 m/s) = 2.85 x 10-8 s
(c) Let Ki be the initial kinetic energy, and solve with basic kinematics.
ΔK/Ki = Δ(1/2 * mev2)/(1/2 * mevi2) = Δv2/vi2 = 2aΔx/vi2 = -2eEΔx/[mevi2]
In this case, we use the new distance of the field given for Δx, 8.00 mm = 8.00 x 10-3 m.
ΔK/Ki= -2(1.60 x 10-19 C)(1.00 x 103 N/C)(8.00 x 10-3 m)/[(9.11 x 10-31 kg)(5.00 x 106 m/s)2] = -0.112
The fraction lost is then 0.112, or 11.2%.
FINAL ANSWERS: (a) 7.12 x 10-2 m
(b) 2.85 x 10-8 s
(c) 0.112, or 11.2%
(b) 2.85 x 10-8 s
(c) 0.112, or 11.2%
•41. A charged cloud system produces an electric field in the air near Earth’s surface. A particle of charge -2.0 x 10-9 C is acted on by a downward
electrostatic force of 3.0 x 10-6 N when placed in this field. (a) What is the magnitude of the electric field? What are the (b) magnitude and (c) direction of the electrostatic
force on the proton placed in this field? (d) What is the magnitude of the gravitational force on the proton? (e) What is the ratio Fel/Fg in this case?
A: Because the negatively charged particle is acted on by a downward force, the electric field must be directed upwards.
(a) Use the formula for the electric field at a point.
E = F/q = (3.0 x 10-6 N)/(2.0 x 10-9 C) = 1.5 x 103 N/C
(b) The force due to an electric field is F = qE.
Fel = qE = eE = (1.60 x 10-19 C)(1.5 x 103 N/C) = 2.4 x 10-16 N
(c) Because a proton is positively charged, it will accelerate in the same direction as the electric field - upwards.
(d) Fg = mg = (1.67 x 10-27 kg)(9.80 m/s2) = 1.6 x 10-26 N
(e) Fel/Fg = (2.4 x 10-16 N)/(1.64 x 10-26 N) = 1.5 x 1010
(a) Use the formula for the electric field at a point.
E = F/q = (3.0 x 10-6 N)/(2.0 x 10-9 C) = 1.5 x 103 N/C
(b) The force due to an electric field is F = qE.
Fel = qE = eE = (1.60 x 10-19 C)(1.5 x 103 N/C) = 2.4 x 10-16 N
(c) Because a proton is positively charged, it will accelerate in the same direction as the electric field - upwards.
(d) Fg = mg = (1.67 x 10-27 kg)(9.80 m/s2) = 1.6 x 10-26 N
(e) Fel/Fg = (2.4 x 10-16 N)/(1.64 x 10-26 N) = 1.5 x 1010
FINAL ANSWERS: (a) 1.5 x 103 N/C
(b) 2.4 x 10-16 N
(c) Upward
(d) 1.6 x 10-26 N
(e) 1.5 x 1010
(b) 2.4 x 10-16 N
(c) Upward
(d) 1.6 x 10-26 N
(e) 1.5 x 1010
•42. Humid air breaks down (its molecules become ionized) in an electric field of 3.0 x 106 N/C. In that field, what is the magnitude of the
electrostatic force on (a) an electron and (b) an ion with a single electron missing?
A: The electric force due to an electric field is F = qE. In the case of the electron, q = e. Normally, we might make this negative, but the problem explicitly asks for the "magnitude" of the force, so
we don't worry about it in this case.
Fe = eE = (1.60 x 10-19 C)(3.0 x 106 N/C) = 4.8 x 10-13 N
In an ion missing one electron, the charge is just going to be +e. Since both parts of the problem only ask for the magnitude, the answer is the same in each case.
Fe = eE = (1.60 x 10-19 C)(3.0 x 106 N/C) = 4.8 x 10-13 N
In an ion missing one electron, the charge is just going to be +e. Since both parts of the problem only ask for the magnitude, the answer is the same in each case.
FINAL ANSWERS: (a) 4.8 x 10-13 N
(b) 4.8 x 10-13 N
(b) 4.8 x 10-13 N
•43. An electron is released from rest in a uniform electric field of magnitude 2.00 x 104 N/C. Calculate the acceleration of the electron. (Ignore gravitation.)
A: The net force on the electron is equal to the force due to the electric field.
Fnet = Fe
ma = qE = eE --> a = eE/m = (1.60 x 10-19 C)(2.00 x 104 N/C)/(9.11 x 10-31 kg) = 3.51 x 1015 m/s2
Fnet = Fe
ma = qE = eE --> a = eE/m = (1.60 x 10-19 C)(2.00 x 104 N/C)/(9.11 x 10-31 kg) = 3.51 x 1015 m/s2
FINAL ANSWER: 3.51 x 1015 m/s2
•44. An alpha particle (the nucleus of a helium atom) has a massof 6.64 x 10-27 kg and a charge of +2e. What are the (a) magnitude and
(b) direction of the electric field that will balance the gravitational force on the particle?
A: If the electric force is to balance the gravitational force, then both forces' magnitudes must be equal.
Fe = Fg
qE = mg --> E = mg/q = mg/[2e] = (6.64 x 10-27kg)(9.80 m/s2)/[2(1.60 x 10-19 C)] = 2.03 x 10-7 N/C
Since the force of gravity is downward, the electric force, qE, must be upward to balance it out. The problem explicitly tells us that the charge on the particle is positive, and we know that positively charged particles travel in the same direction as the electric field - so the field must be directed upwards as well.
Fe = Fg
qE = mg --> E = mg/q = mg/[2e] = (6.64 x 10-27kg)(9.80 m/s2)/[2(1.60 x 10-19 C)] = 2.03 x 10-7 N/C
Since the force of gravity is downward, the electric force, qE, must be upward to balance it out. The problem explicitly tells us that the charge on the particle is positive, and we know that positively charged particles travel in the same direction as the electric field - so the field must be directed upwards as well.
FINAL ANSWERS: (a) 2.03 x 10-7 N/C
(b) Upward
(b) Upward
•45. An electron on the axis of an electric dipole is 25 nm from the center of the dipole. What is the magnitude of the electrostatic force on the electron if the
dipole moment is 3.6 x 10-29 C•m? Assume that 25 nm is much larger than the separation of the charged particles that form the dipole.
A: The force due to an electric field is F = qE. The electric field at a distance z away from the center of an electric dipole is E = p/[2πε0z3].
F = qE = q(p/[2πε0z3]) = 2kep/z3 = 2(8.99 x 109 N•m2/C2)(1.60 x 10-19 C)(3.6 x 10-29 C•m)/(25 x 10-9 m)3 = 6.6 x 10-15 N
F = qE = q(p/[2πε0z3]) = 2kep/z3 = 2(8.99 x 109 N•m2/C2)(1.60 x 10-19 C)(3.6 x 10-29 C•m)/(25 x 10-9 m)3 = 6.6 x 10-15 N
FINAL ANSWER: 6.6 x 10-15 N
•46. An electron is accelerated eastward at 1.80 x 109 m/s2 by an electric field. Determine the field (a) magnitude and (b) direction.
A: The formula for the electric field, with q = -e, can be written as
E = F/q = ma/(-e) = -(ma)/e
Let's now solve for the electric field, taking "eastward" to be the positive x direction.
E = -(ma)/e = -(9.11 x 10-31 kg)(1.80 x 109 m/s2)i/(1.60 x 10-19 C) = (-0.0102 N/C)i
Since the field vector is negative, that means it's directed westward.
E = F/q = ma/(-e) = -(ma)/e
Let's now solve for the electric field, taking "eastward" to be the positive x direction.
E = -(ma)/e = -(9.11 x 10-31 kg)(1.80 x 109 m/s2)i/(1.60 x 10-19 C) = (-0.0102 N/C)i
Since the field vector is negative, that means it's directed westward.
FINAL ANSWERS: (a) -0.0102 N/C
(b) Westward
(b) Westward
•47. Beams of high-speed protons can be produced in “guns” using electric fields to accelerate the protons. (a) What acceleration would a
proton experience if the gun’s electric field were 2.00 x 104 N/C? (b) What speed would the proton attain if the field accelerated the proton through a distance of 1.00 cm?
A: (a) Based on Newton's second law, the acceleration a particle experiences due to a force is a = F/m. Since that force is due to an electric field, this becomes a = qE/m, or eE/m, because the charge
is a proton (a proton has a charge of +e).
a = eE/m = (1.60 x 10-19 C)(2.00 x 104 N/C)/(1.67 x 10-27 kg) = 1.92 x 1012 m/s2
(b) When a constant acceleration is assumed, we can determine the final speed by considering the "v squared" kinematics equation, v2 - v02= 2ax. If the electron is starting from rest, this becomes v2 = 2ax, or v = sqrt[2ax]. Plug in values to find v.
v = sqrt[2ax] = sqrt[2(1.92 x 1012 m/s2)(0.0100 m)] = 1.96 x 105 m/s
a = eE/m = (1.60 x 10-19 C)(2.00 x 104 N/C)/(1.67 x 10-27 kg) = 1.92 x 1012 m/s2
(b) When a constant acceleration is assumed, we can determine the final speed by considering the "v squared" kinematics equation, v2 - v02= 2ax. If the electron is starting from rest, this becomes v2 = 2ax, or v = sqrt[2ax]. Plug in values to find v.
v = sqrt[2ax] = sqrt[2(1.92 x 1012 m/s2)(0.0100 m)] = 1.96 x 105 m/s
FINAL ANSWERS: (a) 1.92 x 1012 m/s2
(b) 1.96 x 105 m/s
(b) 1.96 x 105 m/s
A Dipole in an Electric Field
•56. An electric dipole consists of charges +2e and -2e separated by 0.78 nm. It is in an electric field of strength 3.4 x 106 N/C. Calculate the
magnitude of the torque on the dipole when the dipole moment is (a) parallel to, (b) perpendicular to, and (c) antiparallel to the electric field.
A: The formula for torque on an electric dipole due to an electric field is the cross product of the dipole moment and the electric field.
τ = p × E
Just the magnitude can be found as τ = pEsinθ, as per the definition of the cross product.
All that's changing in each part of the problem is the angle, so make sure you know your sine values.
(a) When the values are parallel, the angle between them is zero. Sine of zero is equal to zero, so the entire torque is equal to zero.
(b) When the variables are perpendicular, they're at right angles to each other.
τ = pEsin90° = pE = (2)(1.60 x 10-19 C)(0.78 x 10-9 m)(3.4 x 106 N/C) = 8.5 x 10-22 N•m
(c) When the variables are antiparallel, they are at 180° with each other.
τ = pEsin180° = 0
τ = p × E
Just the magnitude can be found as τ = pEsinθ, as per the definition of the cross product.
All that's changing in each part of the problem is the angle, so make sure you know your sine values.
(a) When the values are parallel, the angle between them is zero. Sine of zero is equal to zero, so the entire torque is equal to zero.
(b) When the variables are perpendicular, they're at right angles to each other.
τ = pEsin90° = pE = (2)(1.60 x 10-19 C)(0.78 x 10-9 m)(3.4 x 106 N/C) = 8.5 x 10-22 N•m
(c) When the variables are antiparallel, they are at 180° with each other.
τ = pEsin180° = 0
FINAL ANSWERS: (a) 0
(b) 8.5 x 10-22 N•m
(c) 0
(b) 8.5 x 10-22 N•m
(c) 0
•57. An electric dipole consisting of charges of magnitude 1.50 nC separated by 6.20 μm is in an electric field of strength 1100 N/C.
What are (a) the magnitude of the electric dipole moment and (b) the difference between the potential energies for dipole orientations parallel and antiparallel to E?
A: (a) The electric dipole moment, p, is equal to qd, where "q" is the charge on each pole and "d" is the distance between them. The problem tells us both of these things.
p = qd = (1.50 x 10-9 C)(6.20 x 10-6 m) = 9.30 x 10-15 C•m
(b) The potential energy on a dipole within an electric field is given by U(θ) = -p • E = -pEcosθ. Therefore, a difference in potential energy due to a change in angle θ can be written as
ΔU = U(θ) - U(θ0) = -pE(cosθ - cosθi).
Now apply the values we have given in the problem:
ΔU = U(180°) - U(0) = -pE(cos180° - cos0) = -pE(-1 - 1) = 2pE = 2(9.30 x 10-15 C•m)(1100 N/C) = 2.05 x 10-11 J
p = qd = (1.50 x 10-9 C)(6.20 x 10-6 m) = 9.30 x 10-15 C•m
(b) The potential energy on a dipole within an electric field is given by U(θ) = -p • E = -pEcosθ. Therefore, a difference in potential energy due to a change in angle θ can be written as
ΔU = U(θ) - U(θ0) = -pE(cosθ - cosθi).
ΔU = U(180°) - U(0) = -pE(cos180° - cos0) = -pE(-1 - 1) = 2pE = 2(9.30 x 10-15 C•m)(1100 N/C) = 2.05 x 10-11 J
FINAL ANSWERS: (a) 9.30 x 10-15 C•m
(b) 2.05 x 10-11 J
(b) 2.05 x 10-11 J