This chapter covers Coulomb's Law (electrostatic force acting between two charges), the quantization of charges, and conservation of charge. Unfortunately, this is one of the more tedious chapters
of the book, since a lot of the problems revolve around setting up complex vector additions, and often require advanced algebra and geometry techniques to solve. Unless you have a lot of patience,
I recommend not trying to solve every single question and problem in the chapter.
Part 1: Chapter 21 Conceptual Questions and Problems
Questions1. Figure 21-11 shows four situations in which five charged particles are evenly spaced along an axis. The charge values are indicated except for the central particle,
which has the same charge in all four situations. Rank the situations according to the magnitude of the net electrostatic force on the central particle, greatest first.
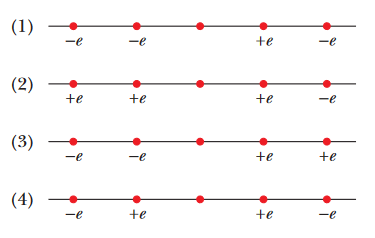

A: In questions like this, it's extremely useful to realize that charges that are positioned with "symmetry" in respect to a central particle will ultimately cancel each other out. For example, let's assume
that the central particle in every case is positive (this will not change our results much; if the central particle was negative, then the forces would just point in the opposite directions).
Take a look at situation (4). If the central particle is positively charged, then the electrostatic force on the central particle due to the positive particles should cancel out. The positive particle on the left will try to repel the central particle to the right, and the positive particle on the right will try to repel the central particle to the left. Since the charges are all equal, these two forces are equal in magnitude and opposite in direction; so they cancel each other out. This same logic can be applied to the negative particles on either side in this situation. All the charges cancel out and the net charge on the central particle in situation (4) is zero.
Let's use take this idea of symmetry and apply it to the other situations as well. In situation (1), the "outer" negative charges cancel each other out. The positive and negative charges closest to the center particle, however, don't cancel each other out, because their forces are pointed in the same direction; the negative charge close to the center will attract the central particle to the left, and the positive particle close to the center will repel the central particle to the left. These forces don't cancel each other out. Let's keep going. In situation (2), the "inner" positively charged particles cancel out, but the outer charges don't. In situation (3), none of the charges cancel each other out, because there is no symmetry with the charges there. The negative charges on the left will attract the central particle left, and the positive charges on the right will repel the central particle left. We can now be sure that situation (3) has the largest magnitude of the net electrostatic force.
We still have to rank situations (1) and (2), however, because we still have a single pair of opposing charges in both cases. We can rank this by considering Coulomb's law; where the electrostatic force between two particles is given as
F = k|q1||q2|/r2
This formula is an example of an inverse square law, because it's inversely proportional to the square of the distance between both particles. This tells us that the magnitude of the force will decrease when the particles are farther away from one another. For this reason, we can determine that the net electrostatic force on the central particle is greater in situation (1) than in situation (2), because the particles that haven't been cancelled out are closer to the center in situation (1); this means that the forces acting on the center must add up to a lager force magnitude overall.
Take a look at situation (4). If the central particle is positively charged, then the electrostatic force on the central particle due to the positive particles should cancel out. The positive particle on the left will try to repel the central particle to the right, and the positive particle on the right will try to repel the central particle to the left. Since the charges are all equal, these two forces are equal in magnitude and opposite in direction; so they cancel each other out. This same logic can be applied to the negative particles on either side in this situation. All the charges cancel out and the net charge on the central particle in situation (4) is zero.
Let's use take this idea of symmetry and apply it to the other situations as well. In situation (1), the "outer" negative charges cancel each other out. The positive and negative charges closest to the center particle, however, don't cancel each other out, because their forces are pointed in the same direction; the negative charge close to the center will attract the central particle to the left, and the positive particle close to the center will repel the central particle to the left. These forces don't cancel each other out. Let's keep going. In situation (2), the "inner" positively charged particles cancel out, but the outer charges don't. In situation (3), none of the charges cancel each other out, because there is no symmetry with the charges there. The negative charges on the left will attract the central particle left, and the positive charges on the right will repel the central particle left. We can now be sure that situation (3) has the largest magnitude of the net electrostatic force.
We still have to rank situations (1) and (2), however, because we still have a single pair of opposing charges in both cases. We can rank this by considering Coulomb's law; where the electrostatic force between two particles is given as
F = k|q1||q2|/r2
This formula is an example of an inverse square law, because it's inversely proportional to the square of the distance between both particles. This tells us that the magnitude of the force will decrease when the particles are farther away from one another. For this reason, we can determine that the net electrostatic force on the central particle is greater in situation (1) than in situation (2), because the particles that haven't been cancelled out are closer to the center in situation (1); this means that the forces acting on the center must add up to a lager force magnitude overall.
FINAL ANSWER: 3, 1, 2, 4
Problems
Coulomb's Law
•1. Of the charge Q initially on a tiny sphere, a portion q is to be transferred to a second, nearby sphere. Both spheres
can be treated as particles and are fixed with a certain separation. For what value of q/Q will the electrostatic force
between the two spheres be maximized?
A: The first charge, "Q", is losing an amount of charge "q" to another particle. The charges of each sphere are now
"Q - q" and "q". The electrostatic force between them can be set up using Coulomb's Law:
F = k|q1||q2|/r2 = k(Q - q)(q)/r2 = k(Qq - q2)/r2
Of course, we're trying to maximize the function, so we need to find where the derivative of this function is equal to zero. The only variables we're trying to manipulate are the charges, so we can simplify this entire derivative by only focusing on the "(Qq - q2)" part of the function. After all, if this term is maximized, then the entire function will be maximized (since "k" and "r" are both constant in this situation). Specifically, we want to take the derivative with respect to the q charge rather than Q, because q just represents the amount of charge being removed from Q, while Q is theoretically constant. We take the derivative and set it equal to zero:
f(q) = Qq - q2 --> df/dq = Q - 2q = 0 --> q = Q/2 --> q/Q = 1/2 = 0.500.
We know that this is the maximum and not the minimum because the second derivative of our function becomes -2, indicating that the function is entirely concave down. Therefore, the absolute extremum must be a maximum.
F = k|q1||q2|/r2 = k(Q - q)(q)/r2 = k(Qq - q2)/r2
Of course, we're trying to maximize the function, so we need to find where the derivative of this function is equal to zero. The only variables we're trying to manipulate are the charges, so we can simplify this entire derivative by only focusing on the "(Qq - q2)" part of the function. After all, if this term is maximized, then the entire function will be maximized (since "k" and "r" are both constant in this situation). Specifically, we want to take the derivative with respect to the q charge rather than Q, because q just represents the amount of charge being removed from Q, while Q is theoretically constant. We take the derivative and set it equal to zero:
f(q) = Qq - q2 --> df/dq = Q - 2q = 0 --> q = Q/2 --> q/Q = 1/2 = 0.500.
We know that this is the maximum and not the minimum because the second derivative of our function becomes -2, indicating that the function is entirely concave down. Therefore, the absolute extremum must be a maximum.
FINAL ANSWER: 0.500
•2. Identical isolated conducting spheres 1 and 2 have equal charges and are separated by a distance that is large compared with
their diameters (Fig. 21-22a). The electrostatic force acting on sphere 2 due to sphere 1 is F. Suppose now that a third identical
sphere 3, having an insulating handle and initially neutral, is touched first to sphere 1 (Fig. 21-22b), then to sphere 2 (Fig. 21-22c), and finally
removed (Fig. 21-22d). The electrostatic force that nowacts on sphere 2 has magnitude F′. What is the ratio F′/F?
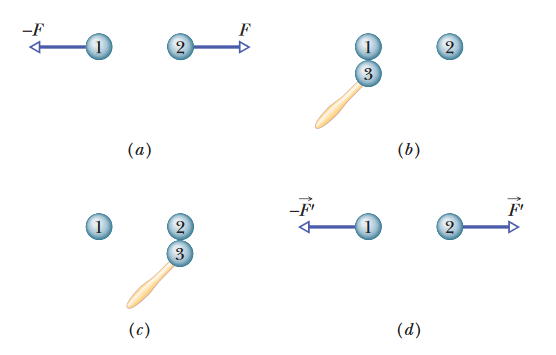

A: First of all, since the problem tells us that both spheres have initially equal charges, let's say that each sphere has a charge of "q".
An important thing to realize about excess charges is that, because they will repel one another, they will tend to be evenly distributed across the entire particle or area. This applies to conducting objects as well; even if the objects are touched together for only a moment, the excess charges will quickly distribute themselves across the entire system of conductors.
Therefore, when the "initially neutral" sphere 3 is touched to the sphere 1 (with a charge of q), the total charge between them will be equally spread throughout both spheres. If the total charge between them is q, then a charge of q/2 will exist in each sphere after the connection.
When sphere 3, now with a charge of q/2, is then touched to sphere 2 (with a charge of q), the total charge shared between them is q + q/2, or 3q/2. The charge in each individual sphere will be half of that, 3q/4. We now have a situation where sphere 1 has a charge of q, and sphere 2 has a charge of 3q/4.
It's now easy to see why the electrostatic forces between spheres 1 & 2 are different before and after the scenario. This can be further demonstrated with the formulas:
F = k|q1||q2|/r2 = k(q)(q)/r2 = kq2/r2
F′ = k|q1||q2|/r2 = k(q/2)(3q/4)/r2 = k(3/8)q2/r2
Now divide F′ by F to find the ratio we're looking for:
F′/F = [k(3/8)q2/r2] / [kq2/r2] = 3/8.
We end up not even having to do any real math there, because the variables all cancel each other out until all that's left is 3/8.
An important thing to realize about excess charges is that, because they will repel one another, they will tend to be evenly distributed across the entire particle or area. This applies to conducting objects as well; even if the objects are touched together for only a moment, the excess charges will quickly distribute themselves across the entire system of conductors.
Therefore, when the "initially neutral" sphere 3 is touched to the sphere 1 (with a charge of q), the total charge between them will be equally spread throughout both spheres. If the total charge between them is q, then a charge of q/2 will exist in each sphere after the connection.
When sphere 3, now with a charge of q/2, is then touched to sphere 2 (with a charge of q), the total charge shared between them is q + q/2, or 3q/2. The charge in each individual sphere will be half of that, 3q/4. We now have a situation where sphere 1 has a charge of q, and sphere 2 has a charge of 3q/4.
It's now easy to see why the electrostatic forces between spheres 1 & 2 are different before and after the scenario. This can be further demonstrated with the formulas:
F = k|q1||q2|/r2 = k(q)(q)/r2 = kq2/r2
F′ = k|q1||q2|/r2 = k(q/2)(3q/4)/r2 = k(3/8)q2/r2
Now divide F′ by F to find the ratio we're looking for:
F′/F = [k(3/8)q2/r2] / [kq2/r2] = 3/8.
We end up not even having to do any real math there, because the variables all cancel each other out until all that's left is 3/8.
FINAL ANSWER: 3/8
•3. What must be the distance between point charge q1 = 26.0 μC and point charge q2 = -47.0 μC for the electrostatic force
between them to have a magnitude of 5.70 N?
We know the force, and we know the charges. We're looking for the distance between them. These are all the relevant variables in the formula for
Coulomb's Law, so let's use that to our advantage. Let's rewrite the Coulomb's Law formula to solve for distance, r, instead of electrostatic force:
F = k|q1||q2|/r2 --> r = sqrt[k|q1||q2|/F] = sqrt[(8.99 x 109 N•m2/C2)(26.0 x 10-6 C)(47.0 x 10-6 C)/(5.70 N)] = 1.39 m
F = k|q1||q2|/r2 --> r = sqrt[k|q1||q2|/F] = sqrt[(8.99 x 109 N•m2/C2)(26.0 x 10-6 C)(47.0 x 10-6 C)/(5.70 N)] = 1.39 m
FINAL ANSWER: 1.39 m
•4. In the return stroke of a typical lightning bolt, a current of 2.5 x 104 A exists for 20 μs. How much charge is transferred in this event?
A: Current is defined as the rate of change of charge with respect to time, or i = dq/dt. If we assume that the current is constant,
then we can also write this as i = q/t. We're explicitly looking for charge here, so solve for q:
i = q/t --> q = it
Plug our information into this simple formula, and make sure to convert 20 microseconds into seconds:
q = it = (2.5 x 104 A)(20 x 10-6 s) = 0.50 C
i = q/t --> q = it
Plug our information into this simple formula, and make sure to convert 20 microseconds into seconds:
q = it = (2.5 x 104 A)(20 x 10-6 s) = 0.50 C
FINAL ANSWER: 0.50 C
•5. A particle of charge +3.00 x 10-6 C is 12.0 cm distant from asecond particle of charge -1.50 x 10-6 C.
Calculate the magnitude of the electrostatic force between the particles.
A: First, convert the 12.0 cm into meters so that we're working with SI units. 12.0 cm = 0.120 m.
Also, we have everything we need to simply plug the information into our Coulomb's Law formula to find the electrostatic force. We have both charges, and the distance between them!
F = k|q1||q2|/r2 = (8.99 x 109 N•m2/C2)(3.00 x 10-6 C)(1.50 x 10-6 C)/(0.120)2 = 2.81 N
Also, we have everything we need to simply plug the information into our Coulomb's Law formula to find the electrostatic force. We have both charges, and the distance between them!
F = k|q1||q2|/r2 = (8.99 x 109 N•m2/C2)(3.00 x 10-6 C)(1.50 x 10-6 C)/(0.120)2 = 2.81 N
FINAL ANSWER: 2.81 N
•6. Two equally charged particles are held 3.2 x 10-3 m apart and then released from rest.
The initial acceleration of the first particle is observed to be 7.0 m/s2 and that of the second to be 9.0 m/s2.
If the mass of the first particle is 6.3 x 10-7 kg, what are
(a) the mass of the second particle and (b) the magnitude of the charge of each particle?
A: (a) Two particles are accelerating due to an electrostatic force between the two particles. Since the particles are accelerating due to the same force,
we can assume that the net forces acting on each of them are equal. Knowing that F = ma, we find:
F12 = F21 --> m1a1 = m2a2 --> m2 = m1a1/a2 = (6.3 x 10-7 kg)(7.0 m/s2)/(9.0 m/s2) = 4.9 x 10-7 kg.
(b) To find the charge on each particle, let's take the formula for Coulomb's Law and solve for q (keeping in mind that both charges are equal):
F = m1a1 = k|q1||q2|/r2 = k|q|2/r2 -->
|q| = sqrt[r2m1a1/k] = sqrt[(3.2 x 10-3)2(6.3 x 10-7 kg)(7.0 m/s2)/(8.99 x 109 N•m2/C2)] |q| = 7.1 x 10-11 C
F12 = F21 --> m1a1 = m2a2 --> m2 = m1a1/a2 = (6.3 x 10-7 kg)(7.0 m/s2)/(9.0 m/s2) = 4.9 x 10-7 kg.
(b) To find the charge on each particle, let's take the formula for Coulomb's Law and solve for q (keeping in mind that both charges are equal):
F = m1a1 = k|q1||q2|/r2 = k|q|2/r2 -->
|q| = sqrt[r2m1a1/k] = sqrt[(3.2 x 10-3)2(6.3 x 10-7 kg)(7.0 m/s2)/(8.99 x 109 N•m2/C2)] |q| = 7.1 x 10-11 C
FINAL ANSWERS: (a) 4.9 x 10-7 kg
(b) 7.1 x 10-11 C
(b) 7.1 x 10-11 C
••7. In Fig. 21-23, three charged particles lie on an x axis. Particles 1 and 2 are fixed in place. Particle 3 is free to move,
but the net electrostatic force on it from particles 1 and 2 happens to be zero. If L23 = L12,
what is the ratio q1/q2?
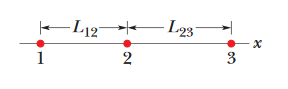
A: First of all, realize that particle 1 and particle 2 must have opposite signs. We know this because of the fact that the net electrostatic
force on particle 3 is zero - if particles 1 and 2 had the same sign, then particle 3 would be attracted toward or repelled away from particles 1 and 2
(theoretically, particle 3 could be in equilibrium with two like charges as long as particle 3 was placed between particles 1 and 2, but the diagram makes it
clear that this is not the case). Therefore, one of the first two particles is positive, and one of them is negative.
Let's set that aside now, but keep it in mind for later.
Ignoring signs for a moment, if the net force on particle 3 from both of the other two particles is zero, then the magnitude of the force from each particle should be equal. We can represent these forces equal to one another using Coulomb's Law:
F31 = F32 --> k|q1||q3|/(L12 + L23)2 = k|q2||q3|/(L23)2
Cancel out the common variables:
|q1|/(L12 + L23)2 = |q2|/(L23)2 --> |q1|/|q2| = (L12 + L23)2/(L23)2
Remember that L23 = L12, so let's substitute L23 in for L12:
|q1|/|q2| = (2L23)2/(L23)2 = 4(L23)2/(L23)2 = 4
We can see now that |q1|/|q2| = 4. This isn't the answer to our question, though - note the "absolute value" symbols. Remember what we said earlier about how the charges have an opposite sign? If this is the case, then one of these charges should actually be negative. Since one charge is negative and one charge is positive, the entire ratio will be negative. So the actual answer is negative 4.
Ignoring signs for a moment, if the net force on particle 3 from both of the other two particles is zero, then the magnitude of the force from each particle should be equal. We can represent these forces equal to one another using Coulomb's Law:
F31 = F32 --> k|q1||q3|/(L12 + L23)2 = k|q2||q3|/(L23)2
Cancel out the common variables:
|q1|/(L12 + L23)2 = |q2|/(L23)2 --> |q1|/|q2| = (L12 + L23)2/(L23)2
Remember that L23 = L12, so let's substitute L23 in for L12:
|q1|/|q2| = (2L23)2/(L23)2 = 4(L23)2/(L23)2 = 4
We can see now that |q1|/|q2| = 4. This isn't the answer to our question, though - note the "absolute value" symbols. Remember what we said earlier about how the charges have an opposite sign? If this is the case, then one of these charges should actually be negative. Since one charge is negative and one charge is positive, the entire ratio will be negative. So the actual answer is negative 4.
FINAL ANSWER: -4.00
••8. In Fig. 21-24, three identical conducting spheres initially have the following charges: sphere A, 4Q; sphere B, -6Q; and sphere C, 0.
Spheres A and B are fixed in place, with a center-to-center separation that is much larger than the spheres. Two experiments are conducted. In experiment 1,
sphere C is touched to sphere A and then (separately) to sphere B, and then it is removed. In experiment 2, starting with the same initial states,
the procedure is reversed: Sphere C is touched to sphere B and then (separately) to sphere A, and then it is removed.
What is the ratio of the electrostatic force between A and B at the end of experiment 2 to that at the end of experiment 1?
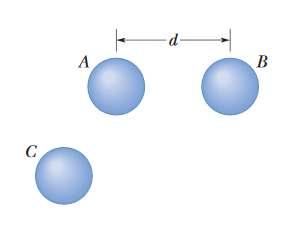

A: This problem is pretty similar to problem #2. The excess charge will equally distribute across conductors that are touching each other.
We can use this to find the final charges in both experiments.
First, in experiment 1, sphere C, with an initial charge of 0 touches sphere A, with a charge 4Q. An equal charge of 2Q is spread to both spheres. Sphere C is then touched to sphere B with a charge of -6Q. Spheres B and C have a total charge together of 2Q + -6Q = -4Q, which is evenly split into -2Q in spheres B and C. The end result of experiment 1 is that sphere A = 2Q and sphere B = -2Q.
In experiment 2, sphere C (0) touches sphere B (-6Q). An equal charge of -3Q is spread to both spheres. Sphere C is then touched to sphere A (4Q). Spheres A and C have a total charge together of 4Q + -3Q = Q, which is evenly split into Q/2 in spheres A and C. The end result of experiment 2 is that sphere A = Q/2 and sphere B = -3Q.
Now let's use Coulomb's Law to find the ratio of the final electrostatic force of experiment 2 to experiment 1:
F2/F1 = k(2Q)(-2Q)/r2 / [k(Q/2)(-3Q)/r2] = (2)(-2) / [(1/2)(-3)] = 0.375
First, in experiment 1, sphere C, with an initial charge of 0 touches sphere A, with a charge 4Q. An equal charge of 2Q is spread to both spheres. Sphere C is then touched to sphere B with a charge of -6Q. Spheres B and C have a total charge together of 2Q + -6Q = -4Q, which is evenly split into -2Q in spheres B and C. The end result of experiment 1 is that sphere A = 2Q and sphere B = -2Q.
In experiment 2, sphere C (0) touches sphere B (-6Q). An equal charge of -3Q is spread to both spheres. Sphere C is then touched to sphere A (4Q). Spheres A and C have a total charge together of 4Q + -3Q = Q, which is evenly split into Q/2 in spheres A and C. The end result of experiment 2 is that sphere A = Q/2 and sphere B = -3Q.
Now let's use Coulomb's Law to find the ratio of the final electrostatic force of experiment 2 to experiment 1:
F2/F1 = k(2Q)(-2Q)/r2 / [k(Q/2)(-3Q)/r2] = (2)(-2) / [(1/2)(-3)] = 0.375
FINAL ANSWER: 0.375
••9. Two identical conducting spheres, fixed in place, attract each other with an electrostatic force of 0.108 N
when their center-to-center separation is 50.0 cm. The spheres are then connected by a thin conducting wire. When the wire is removed,
the spheres repel each other with an electrostatic force of 0.0360 N. Of the initial charges on the spheres, with a positive net charge,
what was (a) the negative charge on one of them and (b) the positive charge on the other?
A: This is a pretty tricky one. We're just asked for "the negative charge" and "the positive charge", so
we have a bit of freedom to arbitrarily define coordinates and signs. In this case, I'll (mostly randomly) define the situation in the following ways:
- q1 and q2 are both along the positive x axis.
- q1 is negative and q2 is positive.
- q2 is further to the "right" on the positive x axis than q1 is.
Now let's try to describe the forces acting on one of the particles (in this case, let's say q2) both before and after the wire plays its role. Let's call the electrostatic force on q2 before the wire appears Fa, and the force on q2 after the wire is removed Fb.
Fa can simply be represented using Coulomb's Law. Note that because the force is attractive, this will be a negative electrostatic force (we aren't going to use the "absolute value" symbols on Coulomb's law in this case, because the system itself is simple enough that we can go with the general rule of signs for electrostatic force: a repulsive force is positive, an attractive force is negative).
Fa = - kq1q2/r2
To write a formula for Fb, let's recall that when two conducting objects are connected, the excess charge will be equally distributed between them. Therefore, the charges on each particle after the fact will be equal to the sum of their total charges, divided between them (or (q1 + q2)/2). The force Fb acting on q2 after the wire is removed can then be represented as the following (and note that since the charges are equal now, including in sign, the force will be repulsive and therefore positive):
Fb = k[(q1 + q2)/2][(q1 + q2)/2]/r2 = k(q1 + q2)2/4r2
Admittedly, this is a little hard to read in text form, but if you're following along by writing this out then it (hopefully) shouldn't be too confusing. This formula is basically just Coulomb's Law but with (q1 + q2)/2 used for both charges (since the charges will be equal after the wire is removed).
We can use these formulas to start getting closer to what we're trying to solve. If we go back to the Fa formula, we can solve for the product of both charges:
Fa = - kq1q2/r2 --> q1q2 = r2Fa/(- k)
We can plug in k, the distance between the spheres, and Fa to find the product of the initial charges:
q1q2 = r2Fa/(- k) = -(0.500 m)2(0.108 N)/(8.99 x 109 N•m2/C2) ≈ -3 x 10-12 C2 (Be sure to preserve the exact value in your calculator for the later calculations)
We can also use the Fb formula to solve for q1 + q2:
Fb = k(q1 + q2)2/4r2 --> q1 + q2 = sqrt[4r2Fb/k] = 2r*sqrt[Fb/k] = 2(0.500 m)sqrt[(0.0360 N)/(8.99 x 109 N•m2/C2)] ≈ 2 x 10-6 C
We now have a system of equations that we can solve for:
(1) q1q2 = -3 x 10-12 C2
(2) q1 + q2 = 2 x 10-6 C
We can now use algebra to solve for this system of equations. We can set the equation (1) equal to q2:
(3) q2 = -3 x 10-12 C2/(q1)
And substitute this into equation (2):
2 x 10-6 C = q1 + q2 = q1 - 3 x 10-12 C2/(q1)
We can cancel out the q1 in the denominator of the last term by multiplying all terms of the formula by q1:
(2 x 10-6 C)q1 = (q1)2 - 3 x 10-12 C2
0 = (q1)2 - (2 x 10-6 C)q1 - 3 x 10-12 C2
We can then use the quadratic formula here to solve for q1 (I won't show that here because trying to represent that in typing is futile. I believe in you though, you can do it). The results we get are 3 x 10-6 C and - 1 x 10-6 C. Because this formula represents q1, and we already defined q1 as the negative charge, then our answer has to be -1 x 10-6 C. This is our negative charge, the answer for (a).
However, you may have noticed that, depending on how we defined our variables, this exact method could have worked for either result - implying that the positive answer we got for the quadratic formula is likely the answer for (b), the positive charge. We can verify this by plugging our result in for equation (3):
q2 = -3 x 10-12 C2/(q1) = -3 x 10-12 C2/(-1 x 10-6 C) = 3 x 10-6 C.
- q1 and q2 are both along the positive x axis.
- q1 is negative and q2 is positive.
- q2 is further to the "right" on the positive x axis than q1 is.
Now let's try to describe the forces acting on one of the particles (in this case, let's say q2) both before and after the wire plays its role. Let's call the electrostatic force on q2 before the wire appears Fa, and the force on q2 after the wire is removed Fb.
Fa can simply be represented using Coulomb's Law. Note that because the force is attractive, this will be a negative electrostatic force (we aren't going to use the "absolute value" symbols on Coulomb's law in this case, because the system itself is simple enough that we can go with the general rule of signs for electrostatic force: a repulsive force is positive, an attractive force is negative).
Fa = - kq1q2/r2
To write a formula for Fb, let's recall that when two conducting objects are connected, the excess charge will be equally distributed between them. Therefore, the charges on each particle after the fact will be equal to the sum of their total charges, divided between them (or (q1 + q2)/2). The force Fb acting on q2 after the wire is removed can then be represented as the following (and note that since the charges are equal now, including in sign, the force will be repulsive and therefore positive):
Fb = k[(q1 + q2)/2][(q1 + q2)/2]/r2 = k(q1 + q2)2/4r2
Admittedly, this is a little hard to read in text form, but if you're following along by writing this out then it (hopefully) shouldn't be too confusing. This formula is basically just Coulomb's Law but with (q1 + q2)/2 used for both charges (since the charges will be equal after the wire is removed).
We can use these formulas to start getting closer to what we're trying to solve. If we go back to the Fa formula, we can solve for the product of both charges:
Fa = - kq1q2/r2 --> q1q2 = r2Fa/(- k)
We can plug in k, the distance between the spheres, and Fa to find the product of the initial charges:
q1q2 = r2Fa/(- k) = -(0.500 m)2(0.108 N)/(8.99 x 109 N•m2/C2) ≈ -3 x 10-12 C2 (Be sure to preserve the exact value in your calculator for the later calculations)
We can also use the Fb formula to solve for q1 + q2:
Fb = k(q1 + q2)2/4r2 --> q1 + q2 = sqrt[4r2Fb/k] = 2r*sqrt[Fb/k] = 2(0.500 m)sqrt[(0.0360 N)/(8.99 x 109 N•m2/C2)] ≈ 2 x 10-6 C
We now have a system of equations that we can solve for:
(1) q1q2 = -3 x 10-12 C2
(2) q1 + q2 = 2 x 10-6 C
We can now use algebra to solve for this system of equations. We can set the equation (1) equal to q2:
(3) q2 = -3 x 10-12 C2/(q1)
And substitute this into equation (2):
2 x 10-6 C = q1 + q2 = q1 - 3 x 10-12 C2/(q1)
We can cancel out the q1 in the denominator of the last term by multiplying all terms of the formula by q1:
(2 x 10-6 C)q1 = (q1)2 - 3 x 10-12 C2
0 = (q1)2 - (2 x 10-6 C)q1 - 3 x 10-12 C2
We can then use the quadratic formula here to solve for q1 (I won't show that here because trying to represent that in typing is futile. I believe in you though, you can do it). The results we get are 3 x 10-6 C and - 1 x 10-6 C. Because this formula represents q1, and we already defined q1 as the negative charge, then our answer has to be -1 x 10-6 C. This is our negative charge, the answer for (a).
However, you may have noticed that, depending on how we defined our variables, this exact method could have worked for either result - implying that the positive answer we got for the quadratic formula is likely the answer for (b), the positive charge. We can verify this by plugging our result in for equation (3):
q2 = -3 x 10-12 C2/(q1) = -3 x 10-12 C2/(-1 x 10-6 C) = 3 x 10-6 C.
FINAL ANSWERS: (a) -1 x 10-6 C
(b) 3 x 10-6 C
(b) 3 x 10-6 C
••10. In Fig. 21-25, four particles form a square. The charges are q1 = q4 = Q and q2 = q3 = q.
(a) What is Q/q if the net electrostatic force on particles 1 and 4 is zero?
(b) Is there any value of q that makes the net electrostatic force on each of the four particles zero? Explain.
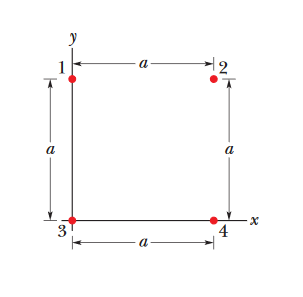

A: First off, let's realize that Q and q must have oppposite signs. Based on that diagram, particles 1 and 4 should be pushing away from each other
due to their like charges, so if particles 1 and 4 are in equilibrium (net force of zero), then a charge with an opposite sign from particles 2 and 3 must be pulling
on particles 1 and 4, keeping them in place. I will arbitrarily choose Q to be positive and q to be negative.
(a) Let's focus on the individual forces acting on either particle 1 or particle 4. Due to the symmetry of the problem, the forces acting on both particles will be equal, so we only need to worry about one of them. I'll look at particle 1. It is also worth noting that, because electrostatic force obeys the law of superposition, we can show the net electrostatic force acting on particle 1 as equal to the force acting on it from each individual particle. That is,
F1 = F12 + F13 + F14 = 0
Once again, the symmetry of this problem makes things pretty easy on us, since we can just focus on either the x components or the y components of the forces acting on the particle and we'll be able to solve for the ratio we want to find. Let's take the superposition formula above and rewrite it to only include the forces exerting a horizontal electrostatic force on particle 1:
F1,x = F12 - F14cos45° = 0.
Notice that the contributions from F13 disappear entirely because of how it's positioned vertically with particle 1, and how the cos45° indicates that we're only using the horizontal component of F14. Also note that F14cos45° is negative, because that force will accelerate particle 1 to the left. We can expand the formulas for the forces using Coulomb's Law:
F1,x = k|q||Q|/a2 - k|Q||Q|cos45°/(a*sqrt[2])2 = 0
The "a*sqrt[2]" comes from using the pythagorean theorem to find the distance between particles 1 and 4. Since the whole thing is squared, it can be rewritten as 2a2. We can use the formula above to solve for Q/q:
k|q||Q|/a2 = k|Q||Q|cos45°/(2a2)
|q| = |Q|/(2) * cos45° = |Q|/2 * sqrt(2)/2 = |Q| * sqrt(2)/4 (where cos45° = sqrt(2)/2)
|Q|/|q| = 4/sqrt(2) = 2.83.
Of course, keep in mind that we're dealing with absolute values here. Remember that both charges have opposite signs (namely, Q is positive and q is negative), so the ratio is actually -2.83.
(b) Now we're looking for the possibility of a value for q. Let's take a look at the net force acting on q2; after all, if there is a value of q that makes the net electrostatic force on all four particles zero, then the ratio we found for part (a) should hold true for every particle. It should also hold true for every component of the forces on every particle, so let's find the y component of the force instead of the x component, to really thoroughly test out our configuration. Once again, this should be equal to the x components we've found elsewhere, or else the value doesn't exist.
Taking the y components of the forces on particle 2, using a similar method to the one we used before:
F2,y = F23sin45° - F24 = 0
F23sin45° is the y component of F23, F21 is disregarded because it doesn't exert a force on particle 2 in the y direction, and F24 is negative because it will pull particle 2 downwards. Let's now apply Coulomb's Law, again in a manner similar to part (a):
k|q||q|sin45°/(2a2) = k|q||Q|/a2
|q|sin45°/(2) = |Q| --> |q|/(2) * sqrt(2)/2 = |Q| -->
|Q|/|q| = sqrt(2)/4
Removing the absolute value symbols makes this negative, as per the same logic we used in part (a):
Q/q = - sqrt(2)/4 ≈ -0.354.
Notice that this ratio is completely different from the one we found in part (a). Because this is the ratio we found by setting the forces in equilibrium, and it doesn't agree with the other ratio we found (also by setting the forces into equilibrium), then this result tells us that this geometry makes it impossible to construct an equilibrium configuration with these charges.
(a) Let's focus on the individual forces acting on either particle 1 or particle 4. Due to the symmetry of the problem, the forces acting on both particles will be equal, so we only need to worry about one of them. I'll look at particle 1. It is also worth noting that, because electrostatic force obeys the law of superposition, we can show the net electrostatic force acting on particle 1 as equal to the force acting on it from each individual particle. That is,
F1 = F12 + F13 + F14 = 0
Once again, the symmetry of this problem makes things pretty easy on us, since we can just focus on either the x components or the y components of the forces acting on the particle and we'll be able to solve for the ratio we want to find. Let's take the superposition formula above and rewrite it to only include the forces exerting a horizontal electrostatic force on particle 1:
F1,x = F12 - F14cos45° = 0.
Notice that the contributions from F13 disappear entirely because of how it's positioned vertically with particle 1, and how the cos45° indicates that we're only using the horizontal component of F14. Also note that F14cos45° is negative, because that force will accelerate particle 1 to the left. We can expand the formulas for the forces using Coulomb's Law:
F1,x = k|q||Q|/a2 - k|Q||Q|cos45°/(a*sqrt[2])2 = 0
The "a*sqrt[2]" comes from using the pythagorean theorem to find the distance between particles 1 and 4. Since the whole thing is squared, it can be rewritten as 2a2. We can use the formula above to solve for Q/q:
k|q||Q|/a2 = k|Q||Q|cos45°/(2a2)
|q| = |Q|/(2) * cos45° = |Q|/2 * sqrt(2)/2 = |Q| * sqrt(2)/4 (where cos45° = sqrt(2)/2)
|Q|/|q| = 4/sqrt(2) = 2.83.
Of course, keep in mind that we're dealing with absolute values here. Remember that both charges have opposite signs (namely, Q is positive and q is negative), so the ratio is actually -2.83.
(b) Now we're looking for the possibility of a value for q. Let's take a look at the net force acting on q2; after all, if there is a value of q that makes the net electrostatic force on all four particles zero, then the ratio we found for part (a) should hold true for every particle. It should also hold true for every component of the forces on every particle, so let's find the y component of the force instead of the x component, to really thoroughly test out our configuration. Once again, this should be equal to the x components we've found elsewhere, or else the value doesn't exist.
Taking the y components of the forces on particle 2, using a similar method to the one we used before:
F2,y = F23sin45° - F24 = 0
F23sin45° is the y component of F23, F21 is disregarded because it doesn't exert a force on particle 2 in the y direction, and F24 is negative because it will pull particle 2 downwards. Let's now apply Coulomb's Law, again in a manner similar to part (a):
k|q||q|sin45°/(2a2) = k|q||Q|/a2
|q|sin45°/(2) = |Q| --> |q|/(2) * sqrt(2)/2 = |Q| -->
|Q|/|q| = sqrt(2)/4
Removing the absolute value symbols makes this negative, as per the same logic we used in part (a):
Q/q = - sqrt(2)/4 ≈ -0.354.
Notice that this ratio is completely different from the one we found in part (a). Because this is the ratio we found by setting the forces in equilibrium, and it doesn't agree with the other ratio we found (also by setting the forces into equilibrium), then this result tells us that this geometry makes it impossible to construct an equilibrium configuration with these charges.
FINAL ANSWERS: (a) -2.83
(b) No (see explanation above).
(b) No (see explanation above).
••11. In Fig. 21-25, the particles have charges q1 = -q2 = 100 nC and q3 = -q4 = 200 nC, and distance a = 5.0 cm. What are the
(a) x and (b) y components of the net electrostatic force on particle 3?


A: (a) As we've been doing, we can find the net force in either component by summing up the forces from each of the other particles. If you're trying to solve every single one of the problems in this chapter,
then I feel sorry for you, because this process is starting to get old by now (I feel sorry for myself).
F3,x = F31,x + F32,x + F34,x
= 0 + k|q3||q2|/(2a2) * cos45° + k|q3||q4|/a2
F31,x is zero because it has no horizontal component of force acting on particle 3 (both particles are positioned vertically with one another). We can simplify this formula a bit:
F3,x = k|q3|/a2*(|q2|/2 * sqrt(2)/2 + |q4|) = k|q3|/a2*(sqrt(2)|q2|/4 + |q4|)
= (8.99 x 109 N•m2/C2)(200 x 10-9 C)/(0.05 m)2*(sqrt(2)(100 x 10-9 C)/4 + (200 x 10-9 C)) = 0.17 N
(b) We apply this same method to the force in the y direction:
F3,y = F31,y + F32,y + F34,y
= - k|q3||q1|/a2 + k|q3||q2|/(2a2) * sin45° + 0
= k|q3|/a2*(-|q1| + |q2|/2*sqrt(2)/2)
F31,y is negative because both particles 1 and 3 are positive and thus repel, so F31,y is directed downwards.
F3,y = k|q3|/a2*(-|q1| + sqrt(2)|q2|/4)
= (8.99 x 109 N•m2/C2)(200 x 10-9 C)/(0.05 m)2*(-(100 x 10-9) + sqrt(2)(100 x 10-9)/4) = -0.046 N
F3,x = F31,x + F32,x + F34,x
= 0 + k|q3||q2|/(2a2) * cos45° + k|q3||q4|/a2
F31,x is zero because it has no horizontal component of force acting on particle 3 (both particles are positioned vertically with one another). We can simplify this formula a bit:
F3,x = k|q3|/a2*(|q2|/2 * sqrt(2)/2 + |q4|) = k|q3|/a2*(sqrt(2)|q2|/4 + |q4|)
= (8.99 x 109 N•m2/C2)(200 x 10-9 C)/(0.05 m)2*(sqrt(2)(100 x 10-9 C)/4 + (200 x 10-9 C)) = 0.17 N
(b) We apply this same method to the force in the y direction:
F3,y = F31,y + F32,y + F34,y
= - k|q3||q1|/a2 + k|q3||q2|/(2a2) * sin45° + 0
= k|q3|/a2*(-|q1| + |q2|/2*sqrt(2)/2)
F31,y is negative because both particles 1 and 3 are positive and thus repel, so F31,y is directed downwards.
F3,y = k|q3|/a2*(-|q1| + sqrt(2)|q2|/4)
= (8.99 x 109 N•m2/C2)(200 x 10-9 C)/(0.05 m)2*(-(100 x 10-9) + sqrt(2)(100 x 10-9)/4) = -0.046 N
FINAL ANSWERS: (a) 0.17 N
(b) -0.046 N
(b) -0.046 N
••12. Two particles are fixed on an x axis. Particle 1 of charge 40 μC is located at x = -2.0 cm; particle 2 of charge Q is located at x = 3.0 cm. Particle 3 of charge magnitude 20 μC
is released from rest on the y axis at y = 2.0 cm. What is the value of Q if the initial acceleration of particle 3 is in the positive direction of (a) the x axis and (b) the y axis?
A: (a) If the particle was to move in the positive x direction, then the y-components of the net force on its motion should be cancelled out, and it should be attracted to the right.
The situation should look like this:
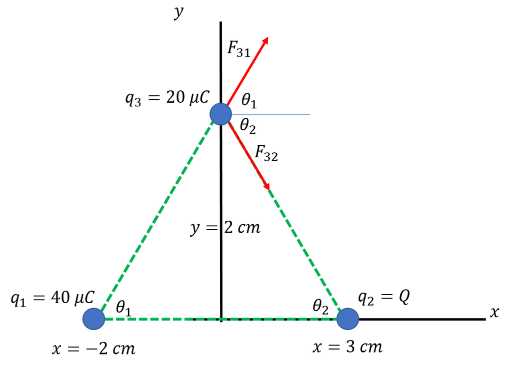
(Note: credit goes to Abdelrahman Almeghari of Slader.com for the visual.)
Q must be negative, so that it attracts particle 3 to the right. It also needs to attract particle 3 downwards so that it cancels out the upwards force on particle 3 due to the presence of particle 1. Our main process here will be to sum the y components of the forces and set that sum equal to zero. Because the particles are angled and form a triangle, we should first find the relevant angles. Based on the diagram:
tan(θ1) = 2/2 = 1 --> θ1= tan-1(1) = 45°
tan(θ2) = 2/3 --> θ2= tan-1(2/3) = 33.7°
Now then, we want the net electrostatic force in the y direction to equal zero.
Fy = F31,y + F32,y = 0
Fy = F31sin(θ1) - F32sin(θ2) = 0
F31sin(θ1) = F32sin(θ2)
Apply Coulomb's law, but also note that the distance between particles 1 and 3 is sqrt[22 + 22] = sqrt(8), and the distance between particles 2 and 3 is sqrt[22 + 32] = sqrt(13).
k|q3||q1|/8 * sin45° = k|q3||Q|/13 * sin33.7°
|q1|/8 * sin45° = |Q|/13 * sin33.7° -->
|Q| = 13|q1/8 * sin45°/sin33.7° = 13(40 x 10-6 C)/8 * sin45°/sin33.7° = 8.3 x 10-5 C = 83 μC
Remember that this is only an absolute value calculation. As we explained earlier, this must be negative; so Q = -83 μC.
(b) In this case, we want particle 3 to only move in the positive y direction, meaning that the x components of the force from particles 1 and 2 should cancel out. Like so:
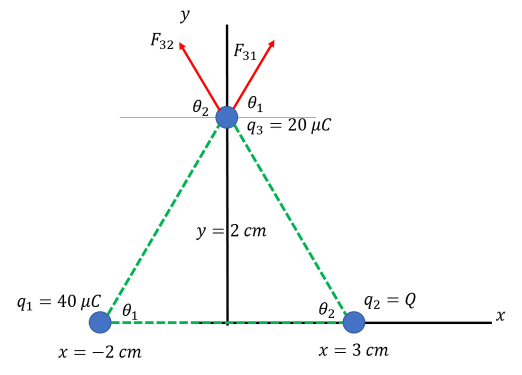
Using a similar process to that of part (a)...
Fx = F31,x + F32,x = 0
F31cos(θ1) - F32cos(θ2) = 0
F31cos(θ1) = F32cos(θ2)
k|q3||q1|/8 * cos(45°) = k|q3||Q|/13 * cos(33.7°)
|q1|/8 * cos(45°) = |Q|/13 * cos(33.7°)
--> |Q| = 13|q1/8 * cos(45°)/cos(33.7°) = 5.5 x 10-5 C = 55 μC
Because the force on particle 3 is directed upwards, this stays positive.

(Note: credit goes to Abdelrahman Almeghari of Slader.com for the visual.)
Q must be negative, so that it attracts particle 3 to the right. It also needs to attract particle 3 downwards so that it cancels out the upwards force on particle 3 due to the presence of particle 1. Our main process here will be to sum the y components of the forces and set that sum equal to zero. Because the particles are angled and form a triangle, we should first find the relevant angles. Based on the diagram:
tan(θ1) = 2/2 = 1 --> θ1= tan-1(1) = 45°
tan(θ2) = 2/3 --> θ2= tan-1(2/3) = 33.7°
Now then, we want the net electrostatic force in the y direction to equal zero.
Fy = F31,y + F32,y = 0
Fy = F31sin(θ1) - F32sin(θ2) = 0
F31sin(θ1) = F32sin(θ2)
Apply Coulomb's law, but also note that the distance between particles 1 and 3 is sqrt[22 + 22] = sqrt(8), and the distance between particles 2 and 3 is sqrt[22 + 32] = sqrt(13).
k|q3||q1|/8 * sin45° = k|q3||Q|/13 * sin33.7°
|q1|/8 * sin45° = |Q|/13 * sin33.7° -->
|Q| = 13|q1/8 * sin45°/sin33.7° = 13(40 x 10-6 C)/8 * sin45°/sin33.7° = 8.3 x 10-5 C = 83 μC
Remember that this is only an absolute value calculation. As we explained earlier, this must be negative; so Q = -83 μC.
(b) In this case, we want particle 3 to only move in the positive y direction, meaning that the x components of the force from particles 1 and 2 should cancel out. Like so:

Using a similar process to that of part (a)...
Fx = F31,x + F32,x = 0
F31cos(θ1) - F32cos(θ2) = 0
F31cos(θ1) = F32cos(θ2)
k|q3||q1|/8 * cos(45°) = k|q3||Q|/13 * cos(33.7°)
|q1|/8 * cos(45°) = |Q|/13 * cos(33.7°)
--> |Q| = 13|q1/8 * cos(45°)/cos(33.7°) = 5.5 x 10-5 C = 55 μC
Because the force on particle 3 is directed upwards, this stays positive.
FINAL ANSWERS: (a) -83 μC
(b) 55 μC
(b) 55 μC
•••20. Figure 21-30a shows an arrangement of three charged particles separated by distance d. Particles A and C are fixed on the x axis, but particle B can be moved along a circle centered on particle A.
During the movement, a radial line between A and B makes an angle θ relative to the positive direction of the x axis (Fig. 21-30b). The curves in Fig. 21-30c give, for two situations, the magnitude Fnet
of the net electrostatic force on particle A due to the other particles. That net force is given as a function of angle θ and as a multiple of a basic amount F0. For example on curve 1, at θ = 180°, we see that
Fnet = 2F0. (a) For the situation corresponding to curve 1, what is the ratio of the charge of particle C to that of particle B (including sign)? (b) For the situation corresponding to curve 2,
what is that ratio?
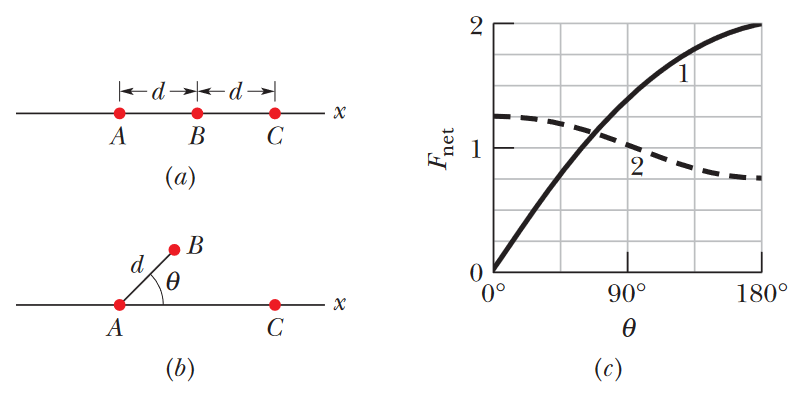
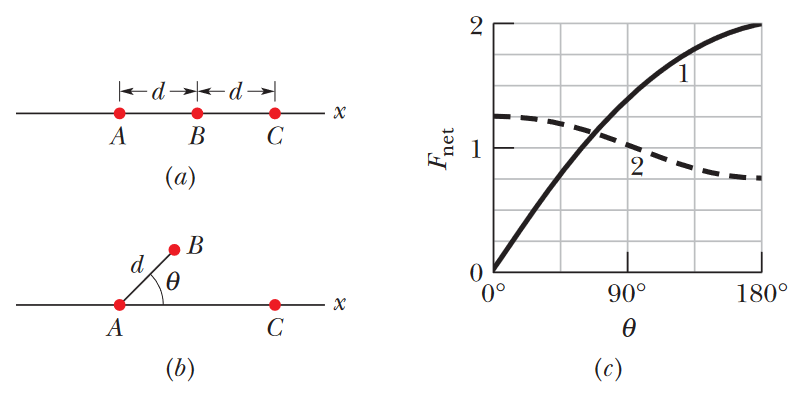
A: A very hard problem. To reiterate, we want to find the ratio of charge C to charge B, based on nothing more than this graph, which actually shows the net force acting just on charge A! In part (a), this
information turns out to be extremely useful, because we can see from this graph that the net force on particle A is maximized when B is at a 180° angle, and the force is zero, -basically completely nonexistent- when B
is at a 0° angle.
Logically speaking, the only way this makes sense is if B and C have opposite signs in their charges. If charge A was positive, for example, then charge B must also be positive, while charge C must be negative. This is because charge B, having the same sign as charge A, will exert a repulsive, leftward force on charge A, which must be counter-acted by an attractive force from an opposite sign, hence charge C being negative. This also fits in with the clue about the force being maximized at 180°, since at 180°, particle B is basically on the opposite side of particle A; The electrostatic forces from particles B and C that cancelled each other out before, will now only amplify each other, since the charge from B will push it in one direction, while the charge from C will pull it further in the same direction. Since charges B and C must have opposite signs, this means that the ratio answer to part (a) must be negative.
We still need to find the magnitude of that ratio. Let's reconsider the case where shown in fig.a here, where the net force is zero. We already explained why these charges must have opposite signs, but the fact that the forces cancel each other out perfectly still must imply that their magnitudes are equal, so that neither of them has an advantage. We can write this as:
FAB = FAC
...indicating that the electrostatic force on particle A from particle B is equal in magnitude to the electrostatic force on particle A from particle C. Since we're looking for a relationship between the charges of B and C, rather than the forces they exert on A, we can rewrite this equality using Coulomb's law, and algebraically solve for the ratio of charge C to charge B.
kqAqB/d2 = kqAqC/(2d)2 (Keep in mind that the distance between particles A and C is twice the distance between A and B)
kqAqB/d2 = kqAqC/(4d2) qB = qC/4 --> qC/ qB = 4
Thus, the magnitude of the ratio of charge C to charge B is 4. Since we've already established that the sign of this ratio is negative, the final value of our ratio is -4.
(b) The next part is a bit harder. Based on the curve for situation (b), we can see that the net electrostatic force on particle A is actually maximized when θ = 0°, and minimized when θ = 180°. This indicates that, no matter where particle B is in its rotation, particle A feels the strongest electrostatic force when particles B and C are both directly to one side of it. Again, using our brains here for a second, this makes the most logical sense if the charges on particles B and C share the same sign. For instance, if charge A is positive, and charges B and C are both negative, then A would be feeling the strongest attractive force at θ = 0°, as both other particles should be pulling it in the same direction. It is therefore safe to conclude that the answer to part (b) will be a positive ratio.
Now to determine the magnitude of this ratio. According to the graph, the net force acting on particle A at θ = 0° is 5F0/4, and the net force at θ = 180° is 3F0/4. In both cases, these net forces are the sum of the individual forces from particles B and C. We can therefore create this system of equations:
(1) 5F0/4 = FAB + FAC
(2) 3F0/4 = FAC - FAB (The force due to particle B is written as negative here because it's positioned on the opposite side of A to where it was in equation (1). Whatever effect it had on particle A in equation (1) will have been reversed here.)
Now we apply Coulomb's law to expand these equations in terms of the charge values:
(1) 5F0/4 = kqAqB/d2 + kqAqC/(4d2) = kqA(4qB + qC)/d2
(2) 3F0/4 = kqAqC/(4d2) - kqAqB/d2 = kqA(qC - 4qB )/d2
Now we've got this system of equations connecting the net force to the charges. To actually solve for the ratio of the charges, we'll need to combine these two equations algebraically. An easy way to do this is to divide one equation by the other. I'll divide equation (1) by equation (2), though it doesn't matter which order you choose:
[5F0/4 = kqA(4qB + qC)/d2] / [3F0/4 = kqA(qC - 4qB )/d2]
[5 = (4qB + qC)] / [3 = (qC - 4qB )] (Cancelling out some common terms)
5/3 = (4qB + qC)/(qC - 4qB )
5qC - 20qB = 12qB + 3qC (Rewriting and simplifying)
2qC = 32qB
qC/qB = 32/2 = 16
So 16 is our ratio. As mentioned earlier, the ratio here must be positive, so we've found our answer.
Logically speaking, the only way this makes sense is if B and C have opposite signs in their charges. If charge A was positive, for example, then charge B must also be positive, while charge C must be negative. This is because charge B, having the same sign as charge A, will exert a repulsive, leftward force on charge A, which must be counter-acted by an attractive force from an opposite sign, hence charge C being negative. This also fits in with the clue about the force being maximized at 180°, since at 180°, particle B is basically on the opposite side of particle A; The electrostatic forces from particles B and C that cancelled each other out before, will now only amplify each other, since the charge from B will push it in one direction, while the charge from C will pull it further in the same direction. Since charges B and C must have opposite signs, this means that the ratio answer to part (a) must be negative.
We still need to find the magnitude of that ratio. Let's reconsider the case where shown in fig.a here, where the net force is zero. We already explained why these charges must have opposite signs, but the fact that the forces cancel each other out perfectly still must imply that their magnitudes are equal, so that neither of them has an advantage. We can write this as:
FAB = FAC
...indicating that the electrostatic force on particle A from particle B is equal in magnitude to the electrostatic force on particle A from particle C. Since we're looking for a relationship between the charges of B and C, rather than the forces they exert on A, we can rewrite this equality using Coulomb's law, and algebraically solve for the ratio of charge C to charge B.
kqAqB/d2 = kqAqC/(2d)2 (Keep in mind that the distance between particles A and C is twice the distance between A and B)
kqAqB/d2 = kqAqC/(4d2) qB = qC/4 --> qC/ qB = 4
Thus, the magnitude of the ratio of charge C to charge B is 4. Since we've already established that the sign of this ratio is negative, the final value of our ratio is -4.
(b) The next part is a bit harder. Based on the curve for situation (b), we can see that the net electrostatic force on particle A is actually maximized when θ = 0°, and minimized when θ = 180°. This indicates that, no matter where particle B is in its rotation, particle A feels the strongest electrostatic force when particles B and C are both directly to one side of it. Again, using our brains here for a second, this makes the most logical sense if the charges on particles B and C share the same sign. For instance, if charge A is positive, and charges B and C are both negative, then A would be feeling the strongest attractive force at θ = 0°, as both other particles should be pulling it in the same direction. It is therefore safe to conclude that the answer to part (b) will be a positive ratio.
Now to determine the magnitude of this ratio. According to the graph, the net force acting on particle A at θ = 0° is 5F0/4, and the net force at θ = 180° is 3F0/4. In both cases, these net forces are the sum of the individual forces from particles B and C. We can therefore create this system of equations:
(1) 5F0/4 = FAB + FAC
(2) 3F0/4 = FAC - FAB (The force due to particle B is written as negative here because it's positioned on the opposite side of A to where it was in equation (1). Whatever effect it had on particle A in equation (1) will have been reversed here.)
Now we apply Coulomb's law to expand these equations in terms of the charge values:
(1) 5F0/4 = kqAqB/d2 + kqAqC/(4d2) = kqA(4qB + qC)/d2
(2) 3F0/4 = kqAqC/(4d2) - kqAqB/d2 = kqA(qC - 4qB )/d2
Now we've got this system of equations connecting the net force to the charges. To actually solve for the ratio of the charges, we'll need to combine these two equations algebraically. An easy way to do this is to divide one equation by the other. I'll divide equation (1) by equation (2), though it doesn't matter which order you choose:
[5F0/4 = kqA(4qB + qC)/d2] / [3F0/4 = kqA(qC - 4qB )/d2]
[5 = (4qB + qC)] / [3 = (qC - 4qB )] (Cancelling out some common terms)
5/3 = (4qB + qC)/(qC - 4qB )
5qC - 20qB = 12qB + 3qC (Rewriting and simplifying)
2qC = 32qB
qC/qB = 32/2 = 16
So 16 is our ratio. As mentioned earlier, the ratio here must be positive, so we've found our answer.
FINAL ANSWERS: (a) -4
(b) 16
(b) 16
Charge Is Quantized
•24. Two tiny, spherical water drops, with identical charges of -1.00 x 10-16 C, have a center-to-center separation of 1.00 cm. (a) What is the magnitude of the electrostatic force
acting between them? (b) How many excess electrons are on each drop, giving it its charge imbalance?
A: (a) We're given the charges of both drops (both charges are identical), and we have the distance between their centers. We can easily enough plug this into Coulomb's law to find the
electrostatic force acting between them.
F = (8.99 x 109 N•m2/C2)(1.00 x 10-16 C)2/(1.00 x 10-2 m)2 = 8.99 x 10-19 N
(b) Because charge is quantized so that all charges are an integer multiple of the "elementary charge", e, we can find the number of excess electrons by dividing the charge by the elementary charge.
n = -q/e = -(-1.00 x 10-16 C)/(1.60 x 10-19 C) = 625 electrons
F = (8.99 x 109 N•m2/C2)(1.00 x 10-16 C)2/(1.00 x 10-2 m)2 = 8.99 x 10-19 N
(b) Because charge is quantized so that all charges are an integer multiple of the "elementary charge", e, we can find the number of excess electrons by dividing the charge by the elementary charge.
n = -q/e = -(-1.00 x 10-16 C)/(1.60 x 10-19 C) = 625 electrons
FINAL ANSWERS: (a) 8.99 x 10-19 N
(b) 625
(b) 625
•25. How many electrons would have to be removed from a coin to leave it with a charge of +1.0 x 10-7 C?
A: Since all charges are equal to an integer multiple of the elementary charge, as |q| = ne, where n is the number of electrons/protons. We solve for n:
n = |q|/e = (1.0 x 10-7 C)/(1.60 x 10-19 C) = 6.3 x 1011 electrons
n = |q|/e = (1.0 x 10-7 C)/(1.60 x 10-19 C) = 6.3 x 1011 electrons
FINAL ANSWER: 6.3 x 1011
•26. What is the magnitude of the electrostatic force between a singly charged sodium ion (Na+, of charge +e) and an adjacent singly charged chlorine ion
(Cl-, of charge -e) in a salt crystal if their separation is 2.82 x 10-10 m?
A: We're given the magnitude of both charges, and the distance between them, so we simply apply Coulomb's law:
F = ke2/r2 = (8.99 x 109 N•m2/C2)(1.60 x 10-19 C)2/(2.82 x 10-10 m)2 = 2.89 x 10-9 N
F = ke2/r2 = (8.99 x 109 N•m2/C2)(1.60 x 10-19 C)2/(2.82 x 10-10 m)2 = 2.89 x 10-9 N
FINAL ANSWER: 2.89 x 10-9 N
•27. The magnitude of the electrostatic force between two identical ions that are separated by a distance of 5.0 x 10-10 m is 3.7 x 10-9 N. (a) What is the charge
of each ion? (b) How many electrons are “missing” from each ion (thus giving the ion its charge imbalance)?
A: (a) Since the charges are identical, we take Coulomb's law and solve for q:
F = kq2/r2 --> q = r*sqrt[F/k] = (5.0 x 10-10 m)*sqrt[(3.7 x 10-9 N)/(8.99 x 109 N•m2/C2)] = 3.2 x 10-19 C
(b) If n is the number of electrons missing from each ion. This situation follows the rule for charge quantization, q = ne. Solve for n:
n = q/e = (3.2 x 10-19 C)/(1.60 x 10-19 C) = 2
F = kq2/r2 --> q = r*sqrt[F/k] = (5.0 x 10-10 m)*sqrt[(3.7 x 10-9 N)/(8.99 x 109 N•m2/C2)] = 3.2 x 10-19 C
(b) If n is the number of electrons missing from each ion. This situation follows the rule for charge quantization, q = ne. Solve for n:
n = q/e = (3.2 x 10-19 C)/(1.60 x 10-19 C) = 2
FINAL ANSWERS: (a) 3.2 x 10-19 C
(b) 2
(b) 2
•28. A current of 0.300 A through your chest can send your heart into fibrillation, ruining the normal rhythm of heartbeat and disrupting the flow of blood (and thus oxygen)
to your brain. If that current persists for 2.00 min, how many conduction electrons pass through your chest?
A: First of all, let's find out the amount of charge passes through your chest. Using the definition of current:
i = q/t --> q = it = (0.300 C/s)(120 s) = 36.0 C
Now we use charge quantization to find the number of electrons:
n = |q|/e = (36.0 C)/(1.60 x 10-19 C) = 2.25 x 1020 electrons
i = q/t --> q = it = (0.300 C/s)(120 s) = 36.0 C
Now we use charge quantization to find the number of electrons:
n = |q|/e = (36.0 C)/(1.60 x 10-19 C) = 2.25 x 1020 electrons
FINAL ANSWER: 2.25 x 1020
Charge Is Conserved
•36. Electrons and positrons are produced by the nuclear transformations of protons and neutrons known as beta decay. (a) If a proton transforms into a neutron,
is an electron or a positron produced? (b) If a neutron transforms into a proton, is an electron or a positron produced?
A: (a) A single proton has a net positive charge, so the output must also have a net positive charge (according to the law of charge conservation). If a proton transforms into a (neutrally charged)
neutron, then one of the additional outputs must have a positive charge, so that the net charge hasn't changed. Therefore, a positron must be produced.
(b) In this case, we're starting with a neutron (neutral charge), and a proton is produced (positive charge). In order for net charge to be conserved, a negative charge must also be produced to balance out this excess positive charge. The other particle must be an electron, because electrons are negatively charged.
(b) In this case, we're starting with a neutron (neutral charge), and a proton is produced (positive charge). In order for net charge to be conserved, a negative charge must also be produced to balance out this excess positive charge. The other particle must be an electron, because electrons are negatively charged.
FINAL ANSWERS: (a) positron
(b) electron
(b) electron
•37. Identify X in the following nuclear reactions: (a) 1H + 9Be -> X + n; (b) 12C + 1H -> X;
(c) 15N + 1H -> 4He + X. Appendix F will help.
(Note: This problem requires some basic chemistry knowledge that isn't provided by the chapter.)
A: (a) The lowercase 'n' refers to a neutron. The number in the superscript to the left of each letter refers to the atomic mass (in Atomic Mass Units, or daltons) of the atom. This atomic mass is the sum
of the neutrons and protons (collectively called "nucleons") in the atom, that most prominently contribute to the atom's mass. A number of protons in an atom is what identifies the atom itself,
so let's first sum up the protons to figure out what type of atom X must be.
H has 1 proton, and Be has 4 protons. If they reacted together, it becomes an atom with 5 protons; which is B (boron). Since Be has 4 protons, but we're told that it has a mass of 9 u, then that means it has 5 neutrons. Those five neutrons are being distributed across the products of the reaction as well, except for the one being subtracted from "X" (because the reaction formula shows that a neutron is produced separately). This means that four neutrons is being added to the five protons in Boron, and its total mass is 9 u. We then write X as 9B.
(b) This reaction is slightly simpler, because no additional neutrons are being lost. C (carbon) has 6 protons, and H (hydrogen) has 1 proton. The result should then have 7 protons, meaning that it must be Nitrogen, N. Since carbon has 6 protons, but has an atomic mass of 12 u, it must have 6 neutrons. These 6 neutrons should then be added to the nitrogen's mass. 6 + 7 = 13. We write the nitrogen as 13N.
(c) Nitrogen (N) has 7 protons, and hydrogen (H) has 1 proton. The results should have a combined total of 8 protons, but we can see that 2 of those are going to the helium (He) atom, because helium always has 2 protons. X should then have the remaining 6 protons - It must be carbon (C). Because nitrogen has only 7 protons, but the nitrogen atom here has an atomic mass of 15 u, it must have 8 neutrons. Therefore, there should be a total of 8 neutrons in the results. Since helium has 2 protons, but this helium atom has a mass of 4 u, we can infer that 2 of the 8 neutrons is going into the helium atom. The other 6 neutrons are then going into X, along with the 6 protons that we've already established are in X. X can thus be written as 12C.
H has 1 proton, and Be has 4 protons. If they reacted together, it becomes an atom with 5 protons; which is B (boron). Since Be has 4 protons, but we're told that it has a mass of 9 u, then that means it has 5 neutrons. Those five neutrons are being distributed across the products of the reaction as well, except for the one being subtracted from "X" (because the reaction formula shows that a neutron is produced separately). This means that four neutrons is being added to the five protons in Boron, and its total mass is 9 u. We then write X as 9B.
(b) This reaction is slightly simpler, because no additional neutrons are being lost. C (carbon) has 6 protons, and H (hydrogen) has 1 proton. The result should then have 7 protons, meaning that it must be Nitrogen, N. Since carbon has 6 protons, but has an atomic mass of 12 u, it must have 6 neutrons. These 6 neutrons should then be added to the nitrogen's mass. 6 + 7 = 13. We write the nitrogen as 13N.
(c) Nitrogen (N) has 7 protons, and hydrogen (H) has 1 proton. The results should have a combined total of 8 protons, but we can see that 2 of those are going to the helium (He) atom, because helium always has 2 protons. X should then have the remaining 6 protons - It must be carbon (C). Because nitrogen has only 7 protons, but the nitrogen atom here has an atomic mass of 15 u, it must have 8 neutrons. Therefore, there should be a total of 8 neutrons in the results. Since helium has 2 protons, but this helium atom has a mass of 4 u, we can infer that 2 of the 8 neutrons is going into the helium atom. The other 6 neutrons are then going into X, along with the 6 protons that we've already established are in X. X can thus be written as 12C.
FINAL ANSWERS: (a) 9B
(b) 13N
(c) 12C
(b) 13N
(c) 12C