Position, Displacement, and Average Velocity
•1. While driving a car at 90 km/h, how far do you move while your eyes shut for 0.50 s during a hard sneeze?
A: First of all, our units are mismatched. The speed of the car is given in kilometers per hour, but the time duration of our eyes being closed is given in seconds. Let's perform a quick
unit conversion (as per the techniques discussed in Chapter 1):
v = 90 km/h = (90 km/h)(1000 m / 1 km)(1 h / 3600 s) = 25 m/s.
Now, we want to find the distance we move during the 0.50 seconds when our eyes are closed. The formula for average velocity is v = d/t, where d is the distance travelled. Solving for d tells us that d = vt. So we use this formula to find the distance:
d = vt = (25 m/s)(0.50 s) ≈ 13 m
v = 90 km/h = (90 km/h)(1000 m / 1 km)(1 h / 3600 s) = 25 m/s.
Now, we want to find the distance we move during the 0.50 seconds when our eyes are closed. The formula for average velocity is v = d/t, where d is the distance travelled. Solving for d tells us that d = vt. So we use this formula to find the distance:
d = vt = (25 m/s)(0.50 s) ≈ 13 m
FINAL ANSWER: 13 m
•2. Compute your average velocity in the following two cases: (a) You walk 73.2 m at a speed of 1.22 m/s and then run 73.2 m at a speed of 3.05 m/s along a straight track.
(b) You walk for 1.00 min at a speed of 1.22 m/s and then run for 1.00 min at 3.05 m/s along a straight track. (c) Graph x versus t for both cases and indicate how the average velocity is found on the graph.
A: (a) Remember that average velocity is equal to the distance travelled divided by the time elapsed. In part (a), this "total distance" is twice 73.2 m, since we walk that exact distance both to and fro.
The time is a bit trickier, since we're not explicitly given any details about the time in part (a). However, because v = d/t, we can see that t = d/v. This means that we can solve for the time in both parts of the problem
this way. The total time elapsed should be the sum of the times we calculate for each part of the walk.
vavg = d/t = (73.2 m + 73.2 m)/[(73.2 m)/(1.22 m/s) + (73.2 m)/(3.05 m/s)] = 1.74 m/s
(b) This time, we're given the time in each part of the problem, but we don't have the distance. Instead, the v = d/t formula tells us that the distance d = vt. Once again, we apply the average velocity formula:
vavg = d/t = [(1.22 m/s)(60 s) + (3.05 m/s)(60 s)]/(120 s) = 2.14 m/s
(c) The graph of these functions will look like this:
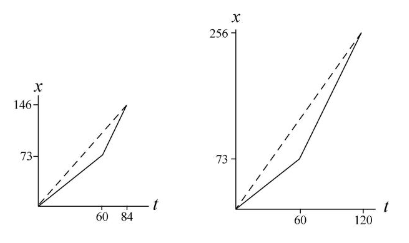
The dotted lines represent the "average velocity" in each case, because they represent the slopes of the change in position over a period of time.
vavg = d/t = (73.2 m + 73.2 m)/[(73.2 m)/(1.22 m/s) + (73.2 m)/(3.05 m/s)] = 1.74 m/s
(b) This time, we're given the time in each part of the problem, but we don't have the distance. Instead, the v = d/t formula tells us that the distance d = vt. Once again, we apply the average velocity formula:
vavg = d/t = [(1.22 m/s)(60 s) + (3.05 m/s)(60 s)]/(120 s) = 2.14 m/s
(c) The graph of these functions will look like this:

The dotted lines represent the "average velocity" in each case, because they represent the slopes of the change in position over a period of time.
FINAL ANSWERS: (a) 1.74 m/s
(b) 2.14 m/s
(c) See diagrams above.
(b) 2.14 m/s
(c) See diagrams above.
•3. An automobile travels on a straight road for 40 km at 30 km/h. It then continues in the same direction for another
40 km at 60 km/h. (a) What is the average velocity
of the car during the full 80 km trip? (Assume that it moves in the positive x direction.) (b) What is the average speed? (c) Graph x versus t and indicate how the average velocity is found on the graph.
A: (a) For the first part of this problem, we apply the same process that we used in the previous problem. The average velocity is represented by the total distance / total time elapsed, so
We have to find the time in each part of the problem. Since v = d/t --> t = d/v, We can find the time it took for both parts of the situation.
t1 = (40 km)/(30 km/h) = 1.33 h
t2 = (40 km)/(60 km/h) = 0.67 h
The total time is 1.33 h + 0.67 = 2.0 h. Since the automobile travels 40 km in both parts, the total distance travelled is 40 km + 40 km = 80 km. We apply the average velocity formula:
vavg = Δx/Δt = (80 km)/(2.0 h) = 40 km/h
(b) The average speed is different from the average velocity because it doesn't take into account the direction of the motion. In a one-dimensional motion problem like this, converting a velocity to a speed is often as easy as making sure that the speed is equal to the absolute value of the velocity (since "negative velocity" is often used in 1D motion problems to indicate a motion along a negative axis). Therefore, all we need to do is make sure that our velocity doesn't have a negative sign ... which it doesn't. So our answer to part (b) is the same as the answer to part (a).
(c) A rough sketch of the trip should look like:
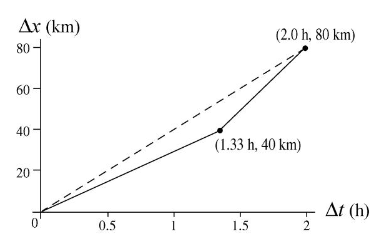
The dotted line represents the average velocity on the graph.
t1 = (40 km)/(30 km/h) = 1.33 h
t2 = (40 km)/(60 km/h) = 0.67 h
The total time is 1.33 h + 0.67 = 2.0 h. Since the automobile travels 40 km in both parts, the total distance travelled is 40 km + 40 km = 80 km. We apply the average velocity formula:
vavg = Δx/Δt = (80 km)/(2.0 h) = 40 km/h
(b) The average speed is different from the average velocity because it doesn't take into account the direction of the motion. In a one-dimensional motion problem like this, converting a velocity to a speed is often as easy as making sure that the speed is equal to the absolute value of the velocity (since "negative velocity" is often used in 1D motion problems to indicate a motion along a negative axis). Therefore, all we need to do is make sure that our velocity doesn't have a negative sign ... which it doesn't. So our answer to part (b) is the same as the answer to part (a).
(c) A rough sketch of the trip should look like:

The dotted line represents the average velocity on the graph.
•4. A car moves uphill at 40 km/h and then back downhill at 60 km/h. What is the average speed for the round trip?
A: A common misconception is to add both velocities together and take the average of those two magnitudes, but this is incorrect - If the car is moving slower uphill than it moves downhill, then
the car is spending more time travelling at 40 km/h than it is at 60 km/h. Therefore, the true average speed should be closer to 40 km/h.
Let's say that D is the distance the car moves either up or down the hill. Because this distance is equal in both parts of the problem, the total distance that the car travels is 2D. Let's apply this to our average velocity formula:
vavg = 2D/[tup + tdown] = 2D/[D/vup + D/vdown]
All the D's will cancel out. Plug in the velocities we have into this formula and we find an average speed of 48 km/h.
Let's say that D is the distance the car moves either up or down the hill. Because this distance is equal in both parts of the problem, the total distance that the car travels is 2D. Let's apply this to our average velocity formula:
vavg = 2D/[tup + tdown] = 2D/[D/vup + D/vdown]
All the D's will cancel out. Plug in the velocities we have into this formula and we find an average speed of 48 km/h.
FINAL ANSWER: 48 km/h
•5. The position of an object moving along an x axis is given by x = 3t - 4t2 + t3, where x is in meters and t in seconds. Find the position of the object at the following
values of t: (a)1 s, (b) 2 s, (c) 3 s, and (d) 4 s. (e) What is the object’s displacement between t = 0 and t = 4 s? (f) What is its average velocity for the time interval from t = 2 s to t = 4 s? (g) Graph x versus t
for 0 ≤ t ≤ 4 s and indicate how the answer for (f) can be found on the graph.
A: We have a formula telling us the position of the object at various points in time, so we can easily find the positions in the first four parts of the problem by plugging the given time values
into the function:
(a) x(1 s) = (3 m/s)(1 s) - (4 m/s2)(1 s)2 + (1 m/s3)(1 s)3 = 0 m
(b) x(2 s) = (3 m/s)(2 s) - (4 m/s2)(2 s)2 + (1 m/s3)(2 s)3 = -2 m
(c) x(3 s) = (3 m/s)(3 s) - (4 m/s2)(3 s)2 + (1 m/s3)(3 s)3 = 0 m
(d) x(4 s) = (3 m/s)(4 s) - (4 m/s2)(4 s)2 + (1 m/s3)(4 s)3 = 12 m
(e) The displacement between two points in time refers to distance between those two positions. The displacement between t = 0 and t = 4 s can be found with
Δx = x(4 s) - x(0) = 12 m - 0 = 12 m
(f) The average velocity is the displacement divided by the time duration of that displacement. The displacement in this case is Δx = x(4 s) - x(2 s) = 12 m - (-2 m) = 14 m. The time elapsed from t = 2 s to t = 4 s is clearly 2 seconds. We now apply the average velocity formula:
vavg = Δx/Δt = (14 m)/(2 s) = 7 m/s
(g) The graph of this function can be easily found with a calculator, though you can also estimate it by individually graphing points at various x positions and estimate the rest. Ultimately, the graph should look something like this:
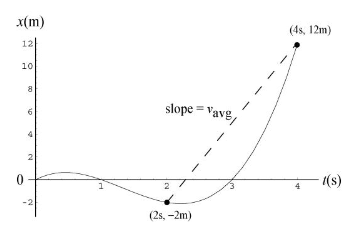
Where the dotted line represents the average velocity between the points at t = 2 s and t = 4 s.
(a) x(1 s) = (3 m/s)(1 s) - (4 m/s2)(1 s)2 + (1 m/s3)(1 s)3 = 0 m
(b) x(2 s) = (3 m/s)(2 s) - (4 m/s2)(2 s)2 + (1 m/s3)(2 s)3 = -2 m
(c) x(3 s) = (3 m/s)(3 s) - (4 m/s2)(3 s)2 + (1 m/s3)(3 s)3 = 0 m
(d) x(4 s) = (3 m/s)(4 s) - (4 m/s2)(4 s)2 + (1 m/s3)(4 s)3 = 12 m
(e) The displacement between two points in time refers to distance between those two positions. The displacement between t = 0 and t = 4 s can be found with
Δx = x(4 s) - x(0) = 12 m - 0 = 12 m
(f) The average velocity is the displacement divided by the time duration of that displacement. The displacement in this case is Δx = x(4 s) - x(2 s) = 12 m - (-2 m) = 14 m. The time elapsed from t = 2 s to t = 4 s is clearly 2 seconds. We now apply the average velocity formula:
vavg = Δx/Δt = (14 m)/(2 s) = 7 m/s
(g) The graph of this function can be easily found with a calculator, though you can also estimate it by individually graphing points at various x positions and estimate the rest. Ultimately, the graph should look something like this:

Where the dotted line represents the average velocity between the points at t = 2 s and t = 4 s.
FINAL ANSWERS: (a) 0 m
(b) -2 m
(c) 0 m
(d) 12 m
(e) 12 m
(f) 7 m/s
(g) See diagram above.
(b) -2 m
(c) 0 m
(d) 12 m
(e) 12 m
(f) 7 m/s
(g) See diagram above.
•6. The 1992 world speed record for a bicycle (human-powered vehicle) was set by Chris Huber. His time through the measured 200 m stretch was a sizzling 6.509 s,
at which he commented, “Cogito ergo zoom!” (I think, therefore I go fast!). In 2001, Sam Whittingham beat Huber’s record by 19.0 km/h. What was Whittingham’s time through the 200 m?
A: First of all, let's find out what Huber's speed actually was. Let's use the velocity formula:
v0 = 200 m / 6.509 s - 30.73 m/s
We want to find Whittingham's speed based on the information we're given. However, we're not actually told what Whittingham's speed was, either. All we know is that his speed was 19.0 km/h faster than Huber's. If we want to find Whittingham's speed, we'll need to add this speed difference to the speed at which Huber travelled. Let's first convert the difference into SI units:
(19 km/h)(1 m/s / 3.6 km/h) ≈ 5.278 m/s
We can now find Whittingham's speed, v1:
v1 = 30.73 m/s + 5.278 m/s = 36.01 m/s
We can now find the time it took for Whittingham to travel 200 m at this speed:
Δt = Δx/v1 = (200 m)/(36.01 m/s) = 5.554 s
v0 = 200 m / 6.509 s - 30.73 m/s
We want to find Whittingham's speed based on the information we're given. However, we're not actually told what Whittingham's speed was, either. All we know is that his speed was 19.0 km/h faster than Huber's. If we want to find Whittingham's speed, we'll need to add this speed difference to the speed at which Huber travelled. Let's first convert the difference into SI units:
(19 km/h)(1 m/s / 3.6 km/h) ≈ 5.278 m/s
We can now find Whittingham's speed, v1:
v1 = 30.73 m/s + 5.278 m/s = 36.01 m/s
We can now find the time it took for Whittingham to travel 200 m at this speed:
Δt = Δx/v1 = (200 m)/(36.01 m/s) = 5.554 s
FINAL ANSWER: 5.554 s
Instantaneous Velocity and Speed
•14. An electron moving along the x axis has a position given by x = 16te-t m, where t is in seconds. How far is the electron
from the origin when it momentarily stops?
A: First of all, we want to find exactly when the electron "momentarily stops"; in other words, whenever its speed is equal to "zero" meters per second. We can find this by taking the derivative of the function
and setting it equal to zero.
v = dx/dt = 16(1 - t)e-t = 0 (Applying the product rule of differentiation here)
We can see that this rate is equal to zero when t = 1 s. Now we know that the electron momentarily stops at this point in time. We can find the electron's position at this point in time by simply plugging this time value into the original function, to get the electron's position based on time.
x = 16(1 s)e-(1 s) = 5.9 m
v = dx/dt = 16(1 - t)e-t = 0 (Applying the product rule of differentiation here)
We can see that this rate is equal to zero when t = 1 s. Now we know that the electron momentarily stops at this point in time. We can find the electron's position at this point in time by simply plugging this time value into the original function, to get the electron's position based on time.
x = 16(1 s)e-(1 s) = 5.9 m
FINAL ANSWER: 5.9 m
•15. (a) If a particle’s position is given by x = 4 - 12t + 3t2 (where t is in seconds and x is in meters), what is its velocity at t = 1 s? (b) Is it moving in the positive or
negative direction of x just then? (c) What is its speed just then? (d) Is the speed increasing or decreasing just then? (Try answering the next two questions without further calculation.) (e)
Is there ever an instant when the velocity is zero? If so, give the time t; if not, answer no. (f) Is there a time after t = 3 s when the particle is moving in the negative direction of x? If so, give the time t; if not,
answer no.
A: (a) We first need to find a formula for the velocity of the particle's motion. Since velocity is defined as the rate of change in position, we first take the derivative of the position formula.
v = dx/dt = -12 + 6t
We now solve this formula for t = 1 s.
v = (-12 + 6(1 s)) = -6 m/s
(b) Because velocity is a vector (and therefore represents a direction as well as a speed), we can determine whether or not a one-dimensional motion is along the positive or negative axis simply by checking whether or not it has a negative value. Since the velocity we found in part (a) is negative, the particle must be moving in the negative x direction.
(c) Speed is a scalar quantity, meaning it refers to the movement of a particle without communicating the direction of the motion. We can easily convert the velocity into a speed by taking the absolute value of the velocity (to get rid of any direction-indicating negative signs).
|v| = |-6 m/s| = 6 m/s
(d) The rate of change of speed is acceleration, which is the second derivative of the position formula (or, the first derivative of the velocity formula).
a = dv/dt = 6
The formula for acceleration is +6, meaning the velocity is constantly increasing, at every point in the motion. However, don't be tricked; the problem is a little more tricky than that. We're asked to find whether or not the speed is increasing, not the velocity. This makes a difference. At the time t = 1 s, the velocity is negative. Since the velocity is increasing, the velocity will become "less negative" (that is, it will approach zero), until it reaches zero and becomes positive. During this time, the magnitude of the velocity is decreasing as the number gets closer to zero. Therefore, the speed is actually decreasing at this point in time.
(e) Yes, this can be inferred from the fact that we found a negative velocity in part (a) of the problem, and we established in part (d) that the particle is constantly positively accelerating. In order for the velocity to go from negative to positive, there must be a point in time when the velocity is zero, a point at which the particle has momentarily stopped moving.
We can find this point in time by setting the velocity equal to zero in our velocity formula.
v = -12 + 6t = 0 --> t = 2 s.
(f) No. We discovered in the previous part that the particle starts increasing speed in the positive x direction at t = 2 s, and we know that the particle is only ever accelerating positively. Therefore, the particle can never be travelling in the negative x direction after t = 2 s.
v = dx/dt = -12 + 6t
We now solve this formula for t = 1 s.
v = (-12 + 6(1 s)) = -6 m/s
(b) Because velocity is a vector (and therefore represents a direction as well as a speed), we can determine whether or not a one-dimensional motion is along the positive or negative axis simply by checking whether or not it has a negative value. Since the velocity we found in part (a) is negative, the particle must be moving in the negative x direction.
(c) Speed is a scalar quantity, meaning it refers to the movement of a particle without communicating the direction of the motion. We can easily convert the velocity into a speed by taking the absolute value of the velocity (to get rid of any direction-indicating negative signs).
|v| = |-6 m/s| = 6 m/s
(d) The rate of change of speed is acceleration, which is the second derivative of the position formula (or, the first derivative of the velocity formula).
a = dv/dt = 6
The formula for acceleration is +6, meaning the velocity is constantly increasing, at every point in the motion. However, don't be tricked; the problem is a little more tricky than that. We're asked to find whether or not the speed is increasing, not the velocity. This makes a difference. At the time t = 1 s, the velocity is negative. Since the velocity is increasing, the velocity will become "less negative" (that is, it will approach zero), until it reaches zero and becomes positive. During this time, the magnitude of the velocity is decreasing as the number gets closer to zero. Therefore, the speed is actually decreasing at this point in time.
(e) Yes, this can be inferred from the fact that we found a negative velocity in part (a) of the problem, and we established in part (d) that the particle is constantly positively accelerating. In order for the velocity to go from negative to positive, there must be a point in time when the velocity is zero, a point at which the particle has momentarily stopped moving.
We can find this point in time by setting the velocity equal to zero in our velocity formula.
v = -12 + 6t = 0 --> t = 2 s.
(f) No. We discovered in the previous part that the particle starts increasing speed in the positive x direction at t = 2 s, and we know that the particle is only ever accelerating positively. Therefore, the particle can never be travelling in the negative x direction after t = 2 s.
FINAL ANSWERS: (a) -6 m/s
(b) negative x direction
(c) 6 m/s
(d) decreasing
(e) Yes, at t = 2 s
(f) No.
(b) negative x direction
(c) 6 m/s
(d) decreasing
(e) Yes, at t = 2 s
(f) No.
•16. The position function x(t) of a particle moving along an x axis is x = 4.0 - 6.0t2, with x in meters and t in seconds. (a) At what time and (b) where does the particle (momentarily)
stop? At what (c) negative time and (d) positive time does the particle pass through the origin? (e) Graph x versus t for the range -5 s to +5 s. (f) To shift the curve rightward on the graph, should we include the
term +20t or the term -20t in x(t)? (g) Does that inclusion increase or decrease the value of x at which the particle momentarily stops?
A: (a) The particle's velocity is represented by the derivative of its position formula.
v = dx/dt = -12t
The particle momentarily stops whenever its velocity is equal to zero. -12t is clearly equal to zero when t = 0 s.
(b) Now that we know when the particle stops, let's plug this time into our original position formula to find out where the particle is located at that point in time.
x = 4.0 - 6.0(0 s)2 = 4.0 m
(c) The origin is located at x = 0, so let's set the position formula to zero and find which t values will give this result.
x = 4.0 - 6.0t2 = 0 --> t2 = 4.0/6.0 --> t = ±0.82 s
The negative value is -0.82 s.
(d) The positive value we found from part (c)'s results was +0.82 s.
(e) Use a graphing calculator, or estimate based on values from the function.
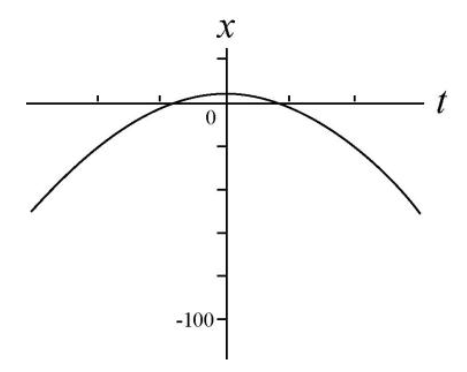
(f) We test out both values in a graphing calculator, and find that +20t shifts the function to the right. It looks like this:
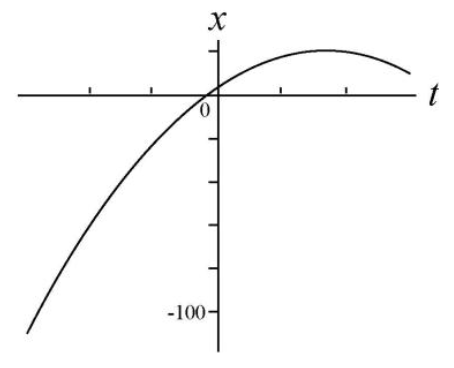
(g) Take a look at the two graphs we've created. Specifically, consider the points where the slopes of the graph become zero (the peaks of the "hills". These are the points where the velocity of the particle momentarily becomes zero. Notice that, after the shift, the v = 0 point now corresponds to a higher value of x. This tells us that the inclusion of +20t increases the x value at which the particle stops.
v = dx/dt = -12t
The particle momentarily stops whenever its velocity is equal to zero. -12t is clearly equal to zero when t = 0 s.
(b) Now that we know when the particle stops, let's plug this time into our original position formula to find out where the particle is located at that point in time.
x = 4.0 - 6.0(0 s)2 = 4.0 m
(c) The origin is located at x = 0, so let's set the position formula to zero and find which t values will give this result.
x = 4.0 - 6.0t2 = 0 --> t2 = 4.0/6.0 --> t = ±0.82 s
The negative value is -0.82 s.
(d) The positive value we found from part (c)'s results was +0.82 s.
(e) Use a graphing calculator, or estimate based on values from the function.

(f) We test out both values in a graphing calculator, and find that +20t shifts the function to the right. It looks like this:

(g) Take a look at the two graphs we've created. Specifically, consider the points where the slopes of the graph become zero (the peaks of the "hills". These are the points where the velocity of the particle momentarily becomes zero. Notice that, after the shift, the v = 0 point now corresponds to a higher value of x. This tells us that the inclusion of +20t increases the x value at which the particle stops.
FINAL ANSWERS: (a) 0 s
(b) 4.0 m
(c) -0.82 s
(d) +0.82 s
(e) See graph above.
(f) +20t
(g) increase
(b) 4.0 m
(c) -0.82 s
(d) +0.82 s
(e) See graph above.
(f) +20t
(g) increase
Acceleration
•18. The position of a particle moving along an x axis is given by x = 12t2 - 2t3, where x is in meters and t is in seconds. Determine (a) the position, (b) the velocity,
and (c) the acceleration of the particle at t = 3.0 s. (d) What is the maximum positive coordinate reached by the particle and (e) at what time is it reached? (f) What is the maximum positive velocity reached by the
particle and (g) at what time is it reached? (h) What is the acceleration of the particle at the instant the particle is not moving (other than at t = 0)? (i) Determine the average velocity of the particle between
t = 0 and t = 3 s.
A: (a) We're given the position formula, so simply plug t = 3.0 s into the formula.
x = 12(3.0 s)2 - 2(3.0 s)3 = 54 m
(b) Now we're looking for the velocity at a point in time, so let's take the derivative of the position formula.
v = dx/dt = 24t - 6t2
Now plug t = 3.0 s into this.
v = 24(3.0 s) - 6(3.0 s)2 = 18 m/s
(c) To find the acceleration at a point, we first take the derivative of the velocity formula.
a = dv/dt = 24 - 12t
Now we plug t = 3.0 s into this.
a = 24 - 12(3.0 s) = -12 m/s2
(d) The acceleration formula suggests that the particle is initially moving in the positive x direction, and is expected to eventually slow down and come to a halt before speeding up again in the negative x direction. Based on this description, we realize that the maximum positive coordinate reached can be found by finding wherever the particle is going to come to a stop, before it reverses its direction. We can find this point in time by setting the velocity formula equal to zero (this will tell us where the particle stops moving).
v = 24t - 6t2 = 0
This formula clearly works when t = 0, but we're specifically referring to the maximum value for t. It's possible that there could be higher values. Let's add the restriction that t cannot be zero, and solve for t again.
24t = 6t2 --> 24 = 6t --> t = 4 s.
The velocity becomes zero when t = 4 s. Let's plug this point in time into the position formula.
x = 12(4 s)2 - 2(4 s)3 = 64 m
(e) As we found in part (d), it reaches this point at t = 4.0 s.
(f) Let's apply the same idea that we used in the previous two parts of the problem. To maximize velocity, let's set acceleration equal to zero and solve for that.
a = 24 - 12t = 0 --> t = 2.0 s
Now let's plug this time value into the formula for velocity.
v = 24(2.0 s) - 6(2.0 s)2 = 24 m/s
(g) As we found in part (f), it reaches this velocity at t = 2.0 s.
(h) In parts (d) and (e), we found that the particle is momentarily motionless at t = 4 s. We now plug this into the acceleration formula.
a = 24 - 12(4 s) = -24 m/s2
(i) Average velocity refers to a change in position over a period of time, and is defined by (x2 - x1)/(t2 - t1). At t = 0, x = 0, and at t = 3 s, x = 54 m (as we found in part (a)).
vavg = (54 m - 0)/(3 s - 0) = 18 m/s.
x = 12(3.0 s)2 - 2(3.0 s)3 = 54 m
(b) Now we're looking for the velocity at a point in time, so let's take the derivative of the position formula.
v = dx/dt = 24t - 6t2
Now plug t = 3.0 s into this.
v = 24(3.0 s) - 6(3.0 s)2 = 18 m/s
(c) To find the acceleration at a point, we first take the derivative of the velocity formula.
a = dv/dt = 24 - 12t
Now we plug t = 3.0 s into this.
a = 24 - 12(3.0 s) = -12 m/s2
(d) The acceleration formula suggests that the particle is initially moving in the positive x direction, and is expected to eventually slow down and come to a halt before speeding up again in the negative x direction. Based on this description, we realize that the maximum positive coordinate reached can be found by finding wherever the particle is going to come to a stop, before it reverses its direction. We can find this point in time by setting the velocity formula equal to zero (this will tell us where the particle stops moving).
v = 24t - 6t2 = 0
This formula clearly works when t = 0, but we're specifically referring to the maximum value for t. It's possible that there could be higher values. Let's add the restriction that t cannot be zero, and solve for t again.
24t = 6t2 --> 24 = 6t --> t = 4 s.
The velocity becomes zero when t = 4 s. Let's plug this point in time into the position formula.
x = 12(4 s)2 - 2(4 s)3 = 64 m
(e) As we found in part (d), it reaches this point at t = 4.0 s.
(f) Let's apply the same idea that we used in the previous two parts of the problem. To maximize velocity, let's set acceleration equal to zero and solve for that.
a = 24 - 12t = 0 --> t = 2.0 s
Now let's plug this time value into the formula for velocity.
v = 24(2.0 s) - 6(2.0 s)2 = 24 m/s
(g) As we found in part (f), it reaches this velocity at t = 2.0 s.
(h) In parts (d) and (e), we found that the particle is momentarily motionless at t = 4 s. We now plug this into the acceleration formula.
a = 24 - 12(4 s) = -24 m/s2
(i) Average velocity refers to a change in position over a period of time, and is defined by (x2 - x1)/(t2 - t1). At t = 0, x = 0, and at t = 3 s, x = 54 m (as we found in part (a)).
vavg = (54 m - 0)/(3 s - 0) = 18 m/s.
FINAL ANSWERS: (a) 54 m
(b) 18 m/s
(c) -12 m/s2
(d) 64 m
(e) 4.0 s
(f) 24 m/s
(g) 2.0 s
(h) -24 m/s2
(i) 18 m/s
(b) 18 m/s
(c) -12 m/s2
(d) 64 m
(e) 4.0 s
(f) 24 m/s
(g) 2.0 s
(h) -24 m/s2
(i) 18 m/s
•19. At a certain time a particle had a speed of 18 m/s in the positive x direction, and 2.4 s later its speed was 30 m/s in the opposite direction. What is the average acceleration of the particle
during this 2.4 s interval?
A: Average acceleration is defined as the change in velocity over a period of time. It's analagous to average velocity, which is a change in position over a course of time. The formulas are pretty
similar, too.
aavg = (v2 - v1)/(t2 - t1)
In this case, t1 18 m/s, and t2 = 30 m/s. The problem tells us that the motion occurs over a course of 2.4 seconds, so t1 = 0, and t2 = 2.4 s. We plug this information into our formula.
aavg = (30 m/s - 18 m/s)/(2.4 s - 0) = -20 m/s2
aavg = (v2 - v1)/(t2 - t1)
In this case, t1 18 m/s, and t2 = 30 m/s. The problem tells us that the motion occurs over a course of 2.4 seconds, so t1 = 0, and t2 = 2.4 s. We plug this information into our formula.
aavg = (30 m/s - 18 m/s)/(2.4 s - 0) = -20 m/s2
FINAL ANSWER: -20 m/s2
•20. (a) If the position of a particle is given by x = 20t - 5t3, where x is in meters and t is in seconds, when, if ever, is the particle’s velocity zero? (b) When is its
acceleration a zero? (c) For what time range (positive or negative) is a negative? (d) Positive? (e) Graph x(t), v(t), and a(t).
A: (a) Let's find the velocity formula by taking the derivative of the position formula, and set it equal to zero.
v = dx/dt = 20 - 15t2 = 0 --> t = sqrt(20/15) = 1.2 s
(b) Now let's take the derivative of the velocity formula and set it equal to zero.
a = dv/dt = -30t = 0 --> t = 0
(c) Because the formula for acceleration is a = -30t, a is always negative when t is positive, and a is always positive when t is negative. The acceleration is neither positive nor negative when t = 0. From this, we can say that the acceleration is negative for t > 0.
(d) As explained in the previous part, the acceleration is positive when t < 0.
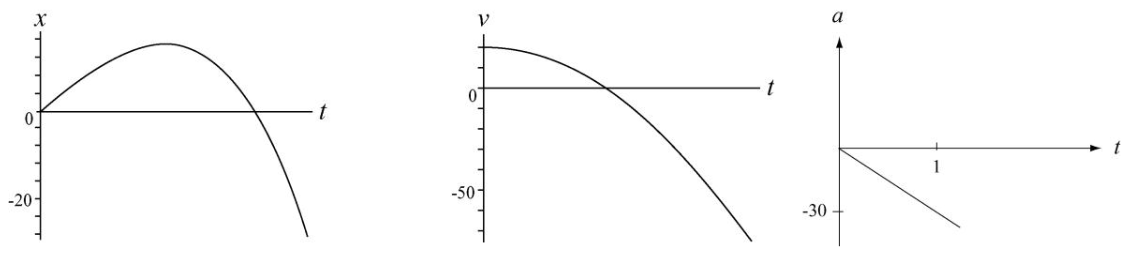
(e) The graphs can be found with a calculator, or by plugging in values and estimating.
v = dx/dt = 20 - 15t2 = 0 --> t = sqrt(20/15) = 1.2 s
(b) Now let's take the derivative of the velocity formula and set it equal to zero.
a = dv/dt = -30t = 0 --> t = 0
(c) Because the formula for acceleration is a = -30t, a is always negative when t is positive, and a is always positive when t is negative. The acceleration is neither positive nor negative when t = 0. From this, we can say that the acceleration is negative for t > 0.
(d) As explained in the previous part, the acceleration is positive when t < 0.
(e) The graphs can be found with a calculator, or by plugging in values and estimating.

FINAL ANSWERS: (a) 1.2 s
(b) 0
(c) t > 0
(d) t < 0
(e) See graphs above.
(b) 0
(c) t > 0
(d) t < 0
(e) See graphs above.
Constant Acceleration
•23. An electron with an initial velocity v0 = 1.50 x 105 m/s enters a region of length L = 1.00 cm where it is electrically accelerated (Fig. 2-26). It emerges
with v = 5.70 x 106 m/s. What is its acceleration, assumed constant?
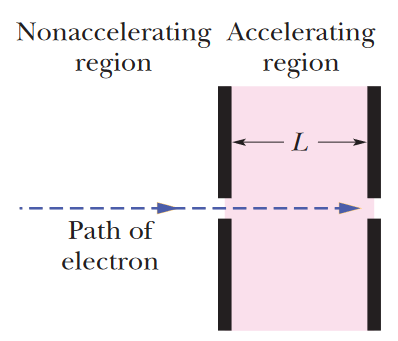

A: In this situation, we have the initial velocity, the final velocity, and the distance along which the acceleration is taking place. We are looking for the acceleration. Careful consideration of the
common kinematics equations tells us that the "v2" equation is probably the best one to use in this case.
v2 = v02 + 2ax --> a = (v2 - v0)/(2x) = [(5.70 x 106 m/s)2 - (1.50 x 105 m/s)2]/[2(0.0100 m)] = 1.62 x 1015 m/s2
v2 = v02 + 2ax --> a = (v2 - v0)/(2x) = [(5.70 x 106 m/s)2 - (1.50 x 105 m/s)2]/[2(0.0100 m)] = 1.62 x 1015 m/s2
FINAL ANSWER: 1.62 x 1015 m/s2
•24. Catapulting mushrooms. Certain mushrooms launch their spores by a catapult mechanism. As water condenses from the air onto a spore that is attached to the mushroom,
a drop grows on one side of the spore and a film grows on the other side. The spore is bent over by the drop’s weight, but when the film reaches the drop, the drop’s water suddenly spreads into the film
and the spore springs upward so rapidly that it is slung off into the air. Typically, the spore reaches a speed of 1.6 m/s in a 5.0 μm launch; its speed is then reduced to zero in 1.0 mm by the air. Using those data
and assuming constant accelerations, find the acceleration in terms of g during (a) the launch and (b) the speed reduction.
A: In both parts of this problem, we solve for an acceleration, but because we're supposed to give both of our answers in terms of g, we must divide each of our final answers by g (9.80 m/s2)
to get the proper answers that the problem is looking for.
(a) During the launch, we have the initial and final velocities (the initial velocity is just zero, since the spore is stationary before it begins accelerating for the catapault), and we have the distance through which the spore accelerates the necessary speed. We want acceleration, so let's use the "v squared" kinematics equation.
v2 = v02 + 2ax --> a = (v2 - v02)/(2x) = (1.6 m/s)2/[2(5.0 x 10-6 m)] = 2.56 x 105 m/s2 = 2.6 x 104 g
(b) For the "speed reduction" phase of the spore's motion, we still have the initial and final speeds, and we have the distance it took to decelerate. We use the same formula to solve for acceleration.
a = (v2 - v02)/(2x) = [0 - (1.6 m/s2)]/[2(1.0 x 10-3 m)] = -1.28 x 103 m/s2 = -1.3 x 102 g
(a) During the launch, we have the initial and final velocities (the initial velocity is just zero, since the spore is stationary before it begins accelerating for the catapault), and we have the distance through which the spore accelerates the necessary speed. We want acceleration, so let's use the "v squared" kinematics equation.
v2 = v02 + 2ax --> a = (v2 - v02)/(2x) = (1.6 m/s)2/[2(5.0 x 10-6 m)] = 2.56 x 105 m/s2 = 2.6 x 104 g
(b) For the "speed reduction" phase of the spore's motion, we still have the initial and final speeds, and we have the distance it took to decelerate. We use the same formula to solve for acceleration.
a = (v2 - v02)/(2x) = [0 - (1.6 m/s2)]/[2(1.0 x 10-3 m)] = -1.28 x 103 m/s2 = -1.3 x 102 g
FINAL ANSWERS: (a) 2.6 x 104 g
(b) -1.3 x 102 g
(b) -1.3 x 102 g
•25. An electric vehicle starts from rest and accelerates at a rate of 2.0 m/s2 in a straight line until it reaches a speed of 20 m/s. The vehicle then slows at a constant rate of
1.0 m/s2 until it stops. (a) How much time elapses from start to stop? (b) How far does the vehicle travel from start to stop?
A: To simplify this problem, we separate the motion into two parts; "part 1", when the vehicle is accelerating to 20 m/s, and "part 2", when the vehicle is decelerating to rest. In part 1, we have
v0 = 0, v = 20 m/s, and a = 2.0 m/s2. In part 2, we have v0 = 20 m/s, v = 0, and a = -1.0 m/s2 (negative because the acceleration vector here points in the
opposite direction to the acceleration in part 1).
(a) To find the time elapsed, we take the amount of time it takes for each part of the motion to occur. When we have the initial/final velocities and the acceleration, and we're looking for the time, we can use the "velocity" kinematics equation.
v = v0 + at
-->
t1 = (v1 - v0,1)/a1 = (20 m/s)/(2.0 m/s2) = 10 s
t2 = (v2 - v0,2)/a2 = (-20 m/s)/(-1.0 m/s2) = 20 s
Now we add these times together. t = t1 + t2 = 10 s + 20 s = 30 s
(b) We now want the total distance that the vehicle travelled. We're still missing the "displacement" variables for each part of the situation, so let's use the "v squared" formula to find that.
v2 = v02 + 2ax
-->
x1 = (v12 - v0,12)/(2a1) = [20 m/s]2/[2(2.0 m/s2)] = 100 m
x2 = (v22 - v0,22)/(2a2) = [-20 m/s]2/[2(-1.0 m/s2)] = 200 m
Now we add these displacements together. x = x1 + x2 = 100 m + 200 m = 300 m
(a) To find the time elapsed, we take the amount of time it takes for each part of the motion to occur. When we have the initial/final velocities and the acceleration, and we're looking for the time, we can use the "velocity" kinematics equation.
v = v0 + at
-->
t1 = (v1 - v0,1)/a1 = (20 m/s)/(2.0 m/s2) = 10 s
t2 = (v2 - v0,2)/a2 = (-20 m/s)/(-1.0 m/s2) = 20 s
Now we add these times together. t = t1 + t2 = 10 s + 20 s = 30 s
(b) We now want the total distance that the vehicle travelled. We're still missing the "displacement" variables for each part of the situation, so let's use the "v squared" formula to find that.
-->
x1 = (v12 - v0,12)/(2a1) = [20 m/s]2/[2(2.0 m/s2)] = 100 m
x2 = (v22 - v0,22)/(2a2) = [-20 m/s]2/[2(-1.0 m/s2)] = 200 m
Now we add these displacements together. x = x1 + x2 = 100 m + 200 m = 300 m
FINAL ANSWERS: (a) 30 s
(b) 300 m
(b) 300 m
•26. A muon (an elementary particle) enters a region with a speed of 5.00 x 106 m/s and then is slowed at the rate of 1.25 x 1014 m/s2.
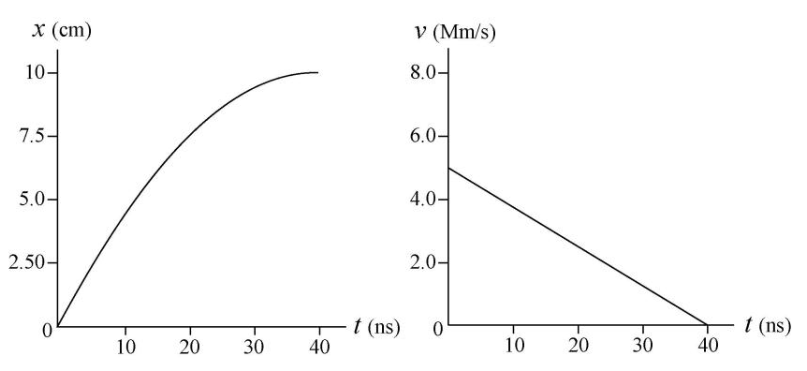
(a) How far does the muon take to stop? (b) Graph x versus t and v versus t for the muon.
A: (a) We have the initial and final velocities (the final velocity is inferred to be "zero" because the problem asks us about when the muon "stops"), and the acceleration rate. We want the distance the muon
travels, so let's use the v-squared formula. I will write the acceleration as negative, because it's a "deceleration" in this case that opposes the motion of the particle.
v2 = v02 + 2ax --> x = (v2 - v02)/(2a) = [02 - (5.00 x 106 m/s)2]/[2(1.25 x 1014 m/s2)] = 0.100 m
(b) The graph of x versus t can be created by using the position formula (x = v0t + 1/2*at2), and using the problem's given values for the acceleration and initial velocity variables. The graph of v versus t can be found by using the velocity formula (v = v0 + at), and once again plugging in the given values for acceleration and initial velocity. The graphs we end up with should look like this:
v2 = v02 + 2ax --> x = (v2 - v02)/(2a) = [02 - (5.00 x 106 m/s)2]/[2(1.25 x 1014 m/s2)] = 0.100 m
(b) The graph of x versus t can be created by using the position formula (x = v0t + 1/2*at2), and using the problem's given values for the acceleration and initial velocity variables. The graph of v versus t can be found by using the velocity formula (v = v0 + at), and once again plugging in the given values for acceleration and initial velocity. The graphs we end up with should look like this:

FINAL ANSWERS: (a) 0.100 m
(b) See graphs and explanation above
(b) See graphs and explanation above
•27. An electron has a constant acceleration of +3.2 m/s2. At a certain instant its velocity is +9.6 m/s. What is its velocity (a) 2.5 s earlier and (b) 2.5 s later?
A: We have the particle's acceleration, its velocity at some point in time, and some time intervals surrounding this point in time. If we set t = 0 at the time when the particle's velocity is
+9.6 m/s, then we can use the velocity formula (v = v0 + at) and treat +9.6 m/s as if it was an initial velocity.
(a) Since we're looking at a time 2.5 s before t = 0, we use negative time for this part.
v = v0 + at = (9.6 m/s) + (3.2 m/s2)(-2.5 s) = 1.6 m/s
(b) Now we're looking at a time 2.5 s after t = 0, so we use positive time here.
v = v0 + at = (9.6 m/s) + (3.2 m/s2)(2.5 s) = 18 m/s
(a) Since we're looking at a time 2.5 s before t = 0, we use negative time for this part.
v = v0 + at = (9.6 m/s) + (3.2 m/s2)(-2.5 s) = 1.6 m/s
(b) Now we're looking at a time 2.5 s after t = 0, so we use positive time here.
v = v0 + at = (9.6 m/s) + (3.2 m/s2)(2.5 s) = 18 m/s
FINAL ANSWERS: (a) 1.6 m/s
(b) 18 m/s
(b) 18 m/s
•28. On a dry road, a car with good tires may be able to brake with a constant deceleration of 4.92 m/s2. (a) How long does such a car, initially traveling at 24.6 m/s,
take to stop? (b) How far does it travel in this time? (c) Graph x versus t and v versus t for the deceleration.
A: Let's assume that the car is travelling in the positive x direction. Since the car is decelerating, the acceleration must be negative; so a = -4.92 m/s2.
(a) We have the final velocity (zero), the initial velocity, and the acceleration. We want to find the time, so we use the velocity formula.
v = v0 + at --> 0 = v0 + at --> t = -v0/a = -(24.6 m/s)/(-4.92 m/s2) = 5.00 s
(b) Now that we've solved for time, we can pretty much use any equation that involves distance, since that's the only variable we're missing. For the sake of the problem, however, I'll use the "v squared" formula, since that's the only option that doesn't depend on our answer to part (a).
0 = v02 + 2ax --> x = - v02/2a = -(24.6 m/s)/[2(4.92 m/s2)] = 61.5 m
(c) We can plot these using the x = v0t + 1/2 * at2 and v = v0 + at formulas.
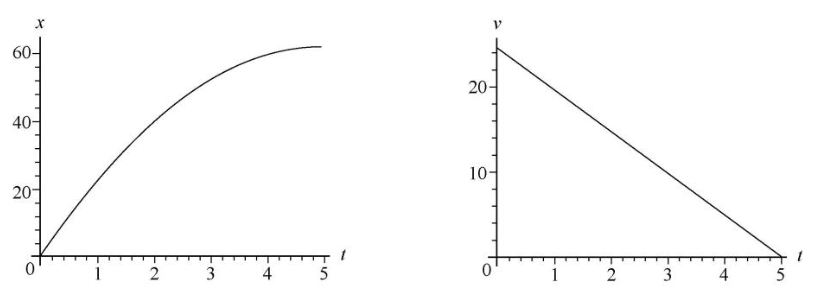
(a) We have the final velocity (zero), the initial velocity, and the acceleration. We want to find the time, so we use the velocity formula.
v = v0 + at --> 0 = v0 + at --> t = -v0/a = -(24.6 m/s)/(-4.92 m/s2) = 5.00 s
(b) Now that we've solved for time, we can pretty much use any equation that involves distance, since that's the only variable we're missing. For the sake of the problem, however, I'll use the "v squared" formula, since that's the only option that doesn't depend on our answer to part (a).
0 = v02 + 2ax --> x = - v02/2a = -(24.6 m/s)/[2(4.92 m/s2)] = 61.5 m
(c) We can plot these using the x = v0t + 1/2 * at2 and v = v0 + at formulas.

FINAL ANSWERS: (a) 5.00 s
(b) 61.5 m
(c) See graphs above.
(b) 61.5 m
(c) See graphs above.
•29. A certain elevator cab has a total run of 190 m and a maximum speed of 305 m/min, and it accelerates from rest and then back to rest at 1.22 m/s2.
(a) How far does the cab move while accelerating to full speed from rest? (b) How long does it take to make the nonstop 190 m run, starting and ending at rest?
A: (a) We have the initial speed (0), the final speed (305 m/min = 5.08 m/s), and the acceleration. We want the distance it takes to reach full speed, so we use the "v squared" equation.
v2 = v02 + 2ax --> x = [v2 - v0]/[2a] = [(5.08 m/s)2 - 02]/[2(1.22 m/s2)] = 10.59 m ≈ 10.6 m
(b) Let t1 be the time it takes for the elevator to accelerate initially, t2 is the time elapsed during the elevator's motion before it starts decelerating, and t3 is when the elevator is decelerating. We can find the time it takes for the elevator to accelerate by using the velocity formula (v = v0 + at).
t = (v - v0)/a = (5.08 m/s)/(1.22 m/s2) = 4.17 s
Because the elevator accelerates and decelerates at the same rate, this must also be the amount of time required for it to slow to rest, too. Therefore, t1 = t3 = 4.17 s. The distance travelled must also be the same for both parts, so the elevator travels 10.59 m in both the acceleration and deceleration. The total distance is 2(10.59 m) = 21.18 m. Since the cab's total run is 190 meters, the missing distance is 190 m - 21.18 m = 168.82 m. The cab must be moving at a constant speed throughout this part. We can find t2 now, assuming a constant velocity.
t2 = (168.82 m)/(5.08 m/s) = 33.21 s
Now we sum the times together to find the total time travelled.
t = t1 + t2 + t3 = 4.17 s + 33.21 s + 4.17 s ≈ 41.5 s
v2 = v02 + 2ax --> x = [v2 - v0]/[2a] = [(5.08 m/s)2 - 02]/[2(1.22 m/s2)] = 10.59 m ≈ 10.6 m
(b) Let t1 be the time it takes for the elevator to accelerate initially, t2 is the time elapsed during the elevator's motion before it starts decelerating, and t3 is when the elevator is decelerating. We can find the time it takes for the elevator to accelerate by using the velocity formula (v = v0 + at).
t = (v - v0)/a = (5.08 m/s)/(1.22 m/s2) = 4.17 s
Because the elevator accelerates and decelerates at the same rate, this must also be the amount of time required for it to slow to rest, too. Therefore, t1 = t3 = 4.17 s. The distance travelled must also be the same for both parts, so the elevator travels 10.59 m in both the acceleration and deceleration. The total distance is 2(10.59 m) = 21.18 m. Since the cab's total run is 190 meters, the missing distance is 190 m - 21.18 m = 168.82 m. The cab must be moving at a constant speed throughout this part. We can find t2 now, assuming a constant velocity.
t2 = (168.82 m)/(5.08 m/s) = 33.21 s
Now we sum the times together to find the total time travelled.
t = t1 + t2 + t3 = 4.17 s + 33.21 s + 4.17 s ≈ 41.5 s
FINAL ANSWERS: (a) 10.6 m
(b) 41.5 s
(b) 41.5 s
•30. The brakes on your car can slow you at a rate of 5.2 m/s2. (a) If you are going 137 km/h and suddenly see a state trooper, what is the minimum time in which you can
get your car under the 90 km/h speed limit? (The answer reveals the futility of braking to keep your high speed from being detected with a radar or laser gun.) (b) Graph
x versus t and v versus t for such a slowing.
A: We have the initial speed (137 km/h = 38.1 m/s), the expected final speed (90 km/h = 25 m/s), and the maximum braking acceleration on the car. We can use the velocity equation
(v = v0 + at) to find the time this deceleration will take. We will write the acceleration as negative in this case, since it opposes the motion.
t = [v - v0]/a = [(25 m/s) - (38.1 m/s)]/(-5.2 m/s2) = 2.5 s
This can be graphed using the position formula (x = v0t + 1/2 * at2).
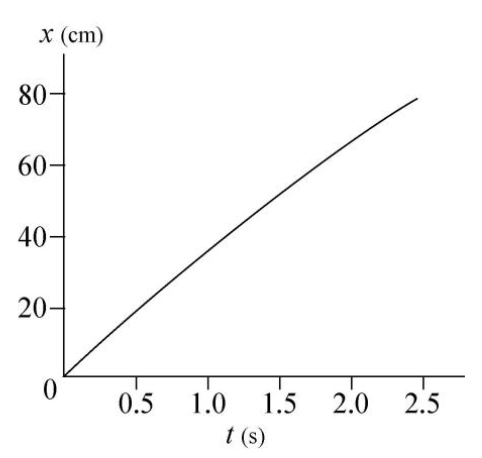
t = [v - v0]/a = [(25 m/s) - (38.1 m/s)]/(-5.2 m/s2) = 2.5 s
This can be graphed using the position formula (x = v0t + 1/2 * at2).

FINAL ANSWERS: (a) 2.5 s
(b) See graph above.
(b) See graph above.
•31. Suppose a rocket ship in deep space moves with constant acceleration equal to 9.8 m/s2, which gives the illusion of normal gravity during the flight.
(a) If it starts from rest, how long will it take to acquire a speed one-tenth that of light, which travels at 3.0 x 108 m/s? (b) How far will it travel in so doing?
A: (a) The speed of light is 3.0 x 108 m/s, so one tenth of that is 3.0 x 107 m/s. This is the final speed we're looking for. We can find the time it takes to reach this speed
using the velocity kinematics equation (v = v0 + at).
t = [v - v0]/a = (3.0 x 107 m/s)/(9.8 m/s2) = 3.1 x 106 s.
(b) We can find the travelled distance by using the position kinematics equation (x = v0t + 1/2 * at2).
x = 0 + 1/2 * (9.8 m/s2)(3.1 x 106 s)2 = 4.6 x 1013 m
t = [v - v0]/a = (3.0 x 107 m/s)/(9.8 m/s2) = 3.1 x 106 s.
(b) We can find the travelled distance by using the position kinematics equation (x = v0t + 1/2 * at2).
x = 0 + 1/2 * (9.8 m/s2)(3.1 x 106 s)2 = 4.6 x 1013 m
FINAL ANSWERS: (a) 3.1 x 106 s.
(b) 4.6 x 1013 m
(b) 4.6 x 1013 m
•32. A world’s land speed record was set by Colonel John P. Stapp when in March 1954 he rode a rocket-propelled sled that moved along a track at 1020 km/h. He and the sled
were brought to a stop in 1.4 s. (See Fig. 2-7.) In terms of g, what acceleration did he experience while stopping?
A: He decelerated from 1020 km/h to rest. We can easily enough use the average acceleration formula to find his acceleration.
a = Δv/Δt = (1020 km/h)(1000 m/km / 3600 s/h)/(1.4 s) = 202.4 m/s2
We want this acceleration in terms of g, however. We divide by g:
a = 202.4 m/s2/(9.80 m/s2) = 21g
a = Δv/Δt = (1020 km/h)(1000 m/km / 3600 s/h)/(1.4 s) = 202.4 m/s2
We want this acceleration in terms of g, however. We divide by g:
a = 202.4 m/s2/(9.80 m/s2) = 21g
FINAL ANSWER: 21g
•33. A car traveling 56.0 km/h is 24.0 m from a barrier when the driver slams on the brakes. The car hits the barrier 2.00 s later. (a) What is the magnitude of the car’s constant acceleration
before impact? (b) How fast is the car traveling at impact?
A: (a) We can use the position formula (x = v0t + 1/2 * at2) to solve for the acceleration.
a = 2(x - v0t)/t2 = 2[(24.0 m) - (15.55 m/s)(2.00 s)]/(2.00 s)2 = -3.56 m/s2
Of course, the absolute value of this is just 3.56 m/s2.
(b) The final speed can be found with the velocity kinematics equation.
v = v0 + at = (15.55 m/s) + (-3.56 m/s2)(2.00 s) = 8.43 m/s
a = 2(x - v0t)/t2 = 2[(24.0 m) - (15.55 m/s)(2.00 s)]/(2.00 s)2 = -3.56 m/s2
Of course, the absolute value of this is just 3.56 m/s2.
(b) The final speed can be found with the velocity kinematics equation.
v = v0 + at = (15.55 m/s) + (-3.56 m/s2)(2.00 s) = 8.43 m/s
FINAL ANSWERS: (a) 3.56 m/s2
(b) 8.43 m/s
(b) 8.43 m/s
••34. In Fig. 2-27, a red car and a green car, identical except for the color, move toward each other in adjacent lanes and parallel to an x axis. At time t = 0, the red car is at xr = 0
and the green car is at xg = 220 m. If the red car has a constant velocity of 20 km/h, the cars pass each other at x = 44.5 m, and if it has a constant velocity of 40 km/h, they pass each other at x = 76.6 m.
What are (a) the initial velocity and (b) the constant acceleration of the green car?


A:
FINAL ANSWERS:
Free-Fall Acceleration
•44. When startled, an armadillo will leap upward. Suppose it rises 0.544 m in the first 0.200 s. (a) What is its initial speed as it leaves the ground? (b) What is its speed
at the height of 0.544 m? (c) How much higher does it go?
A: (a) We assume that the downward acceleration is -g = -9.80 m/s2. We can solve for the initial speed by using the position kinematics formula in the y direction.
y = v0t + 1/2 * at2 --> v0 = [y + gt2/2]/t = [0.544 m + (9.80 m/s2)(0.200 s)2/2]/(0.200 s) = 3.70 m/s
(b) We can now use the velocity kinematics equation (v = v0 + at) to solve for the speed at a certain point in time.
v = v0 - gt = 3.70 m/s - (9.80 m/s2)(0.200 s) = 1.74 m/s
(c) We can find out how high the armadillo actually goes by using the "v squared" formula and setting the final velocity equal to zero (since an object momentarily stops when its at the peak of its motion).
v2 = v02 - 2gy --> y = v02/[2g] = (3.7 m/s)2/[2(9.80 m/s2)] = 0.698 m
y = v0t + 1/2 * at2 --> v0 = [y + gt2/2]/t = [0.544 m + (9.80 m/s2)(0.200 s)2/2]/(0.200 s) = 3.70 m/s
(b) We can now use the velocity kinematics equation (v = v0 + at) to solve for the speed at a certain point in time.
v = v0 - gt = 3.70 m/s - (9.80 m/s2)(0.200 s) = 1.74 m/s
(c) We can find out how high the armadillo actually goes by using the "v squared" formula and setting the final velocity equal to zero (since an object momentarily stops when its at the peak of its motion).
v2 = v02 - 2gy --> y = v02/[2g] = (3.7 m/s)2/[2(9.80 m/s2)] = 0.698 m
FINAL ANSWERS: (a) 3.70 m/s
(b) 1.74 m/s
(c) 0.698 m
(b) 1.74 m/s
(c) 0.698 m
•45. (a) With what speed must a ball be thrown vertically from ground level to rise to a maximum height of 50 m? (b) How long will it be in the air? (c) Sketch graphs of y, v,
and a versus t for the ball. On the first two graphs, indicate the time at which 50 m is reached.
A: (a) To find the final speed based on height, we can use the v-squared kinematics equation (v2 = v02 - 2gy). Keep in mind that at the height of the
ball's motion, v = 0.
v0 = sqrt[2gy] = sqrt[2(9.80 m/s2)(50 m)] = 31.3 m/s
(b) We can use the velocity kinematics equation (v = v0 - gt) to find the time it takes for the ball to reach the peak of its motion.
t = [v0 - v]/g = v0/g
Of course, this is just the time it takes for the ball to reach its height. This doesn't take the fall time into account. Since the same constant acceleration is acting on the ball throughout its entire motion, it should take the same amount of time to fall that it does to rise. Therefore, the total time T will be twice the time formula we found above.
T = 2v0/g = 2(31.3 m/s)/(9.80 m/s2) = 6.39 s
(c) Estimating and graphing the motion of the ball should yield graphs that look roughly like this:
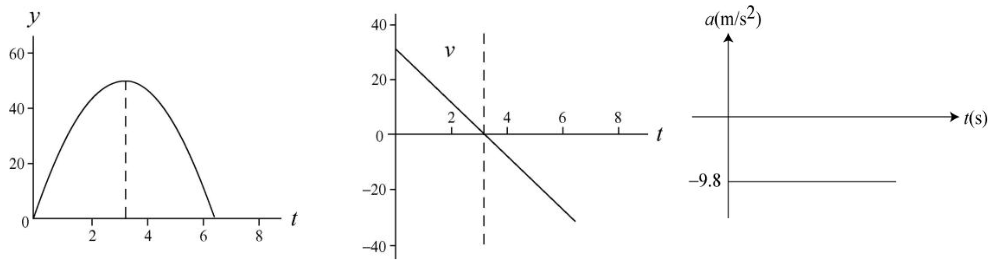
v0 = sqrt[2gy] = sqrt[2(9.80 m/s2)(50 m)] = 31.3 m/s
(b) We can use the velocity kinematics equation (v = v0 - gt) to find the time it takes for the ball to reach the peak of its motion.
t = [v0 - v]/g = v0/g
Of course, this is just the time it takes for the ball to reach its height. This doesn't take the fall time into account. Since the same constant acceleration is acting on the ball throughout its entire motion, it should take the same amount of time to fall that it does to rise. Therefore, the total time T will be twice the time formula we found above.
T = 2v0/g = 2(31.3 m/s)/(9.80 m/s2) = 6.39 s
(c) Estimating and graphing the motion of the ball should yield graphs that look roughly like this:

FINAL ANSWERS: (a) 31.3 m/s
(b) 6.39 s
(c) See graphs above
(b) 6.39 s
(c) See graphs above
•46. Raindrops fall 1700 m from a cloud to the ground. (a) If they were not slowed by air resistance, how fast would the drops be moving when they struck the ground?
(b) Would it be safe to walk outside during a rainstorm?
A: (a) Taking the acceleration to be a = -g, we use the "v squared" formula (v2 = v02 - 2gy). We solve for v, taking the negative root because we know that
the final velocity should be negative.
v = -sqrt[v02 - 2gy] = -sqrt[0 - 2(9.80 m/s2)(-1700 m)] = -183 m/s
The magnitude is then 183 m/s.
(b) It's a little hard to say without more information. 183 m/s isn't as fast as the average bullet, but when it's raining many water droplets travelling this speed at once, getting hit by them could be far more dangerous.
v = -sqrt[v02 - 2gy] = -sqrt[0 - 2(9.80 m/s2)(-1700 m)] = -183 m/s
The magnitude is then 183 m/s.
(b) It's a little hard to say without more information. 183 m/s isn't as fast as the average bullet, but when it's raining many water droplets travelling this speed at once, getting hit by them could be far more dangerous.
FINAL ANSWERS: (a) 183 m/s
(b) Probably not.
(b) Probably not.
•47. At a construction site a pipe wrench struck the ground with a speed of 24 m/s. (a) From what height was it inadvertently dropped? (b) How long was it falling?
(c) Sketch graphs of y, v, and a versus t for the wrench.
A: (a) We can find the height by using the v-squared kinematics equation (v2 = v02 - 2gy).
y = [v02 - v2]/[2g] = [0 - (-24 m/s)2]/[2(9.80 m/s2)] = -29.4 m
The wrench goes through a displacement of -29.4 m in the y direction from an initial height of y = 0. So the wrench falls from a height of 29.4 meters.
(b) We solve for time using v = v0 - gt.
t = [v0 - v]/g = [0 - (-24 m/s)]/9.80 m/s2 = 2.45 s
(c) Using the acceleration due to gravity, we can sketch the motion like this:
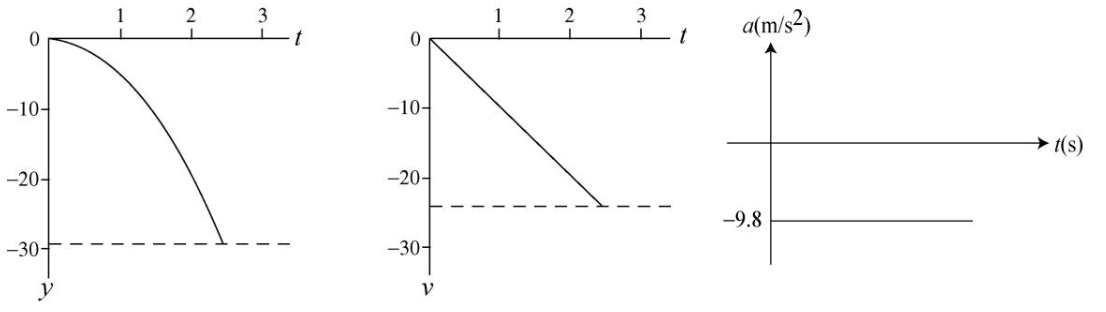
y = [v02 - v2]/[2g] = [0 - (-24 m/s)2]/[2(9.80 m/s2)] = -29.4 m
The wrench goes through a displacement of -29.4 m in the y direction from an initial height of y = 0. So the wrench falls from a height of 29.4 meters.
(b) We solve for time using v = v0 - gt.
t = [v0 - v]/g = [0 - (-24 m/s)]/9.80 m/s2 = 2.45 s
(c) Using the acceleration due to gravity, we can sketch the motion like this:

FINAL ANSWERS: (a) 29.4 m
(b) 2.45 s
(c) See graphs above.
(b) 2.45 s
(c) See graphs above.
•48. A hoodlum throws a stone vertically downward with an initial speed of 12.0 m/s from the roof of a building, 30.0 m above the ground. (a) How long does it take the stone to reach the
ground? (b) What is the speed of the stone at impact?
A: (a) We have the height, the initial velocity, and the acceleration. We want the time, so we can use the position formula (Δy = v0t - 1/2 *gt2).
Using the quadratic formula to solve for t, we find a time of 1.54 s.
(b) Ignoring the result from part (a), we can solve this using the v-squared formula (v2 = v02 - 2gy).
v = sqrt[v02 - 2gy] = sqrt[(12.0 m/s) - 2(9.80 m/s2)(-30.0 m)] = 27.1 m/s
Using the quadratic formula to solve for t, we find a time of 1.54 s.
(b) Ignoring the result from part (a), we can solve this using the v-squared formula (v2 = v02 - 2gy).
v = sqrt[v02 - 2gy] = sqrt[(12.0 m/s) - 2(9.80 m/s2)(-30.0 m)] = 27.1 m/s
FINAL ANSWERS: (a) 1.54 s
(b) 27.1 m/s
(b) 27.1 m/s
•49. A hot-air balloon is ascending at the rate of 12 m/s and is 80 m above the ground when a package is dropped over the side. (a) How long does the package take to reach the ground?
(b) With what speed does it hit the ground?
A: (a) Taking the initial velocity to be +12 m/s, but with a negative acceleration, we can find the time using the position kinematics equation, (Δy = v0t - 1/2 *gt2).
Using the quadratic formula with the values given by the problem, we get a time of 5.45 s.
(b) We can find the final velocity using the velocity equation (v = v0 - gt).
v = (12 m/s) - (9.80 m/s2)(5.447 s) = -41.38 m/s
Of course, the final speed that the problem asks for should be the absolute value of this.
Using the quadratic formula with the values given by the problem, we get a time of 5.45 s.
(b) We can find the final velocity using the velocity equation (v = v0 - gt).
v = (12 m/s) - (9.80 m/s2)(5.447 s) = -41.38 m/s
Of course, the final speed that the problem asks for should be the absolute value of this.
FINAL ANSWERS: (a) 5.45 s
(b) 41.38 m/s
(b) 41.38 m/s
Graphical Integration in Motion Analysis
•65. Figure 2-15a gives the acceleration of a volunteer’s head and torso during a rear-end collision. At maximum head acceleration, what is the speed of (a) the head and (b) the torso?
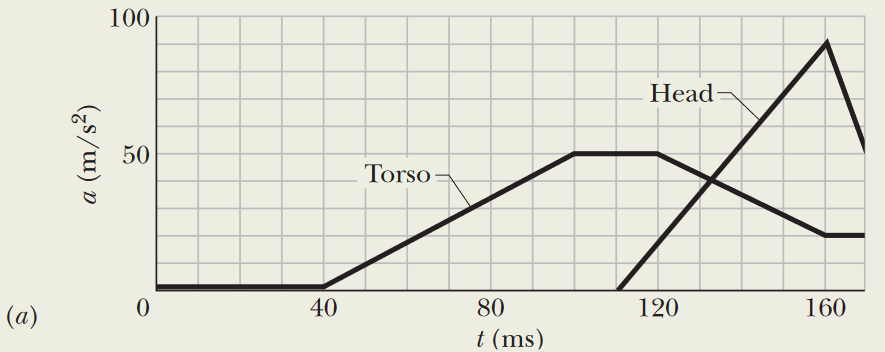

A: Because of the way integration works, we can find the definite integral of a graphed function by calculating the area "under the curve". In other words, we can find the speed of a motion
using an acceleration graph by finding the area underneath the function at that point in time. We can see from the graph that the maximum head acceleration is at t = 160 ms.
(a) Focusing on the head's acceleration function, the graph resembles a triangle at t = 160 ms. We use the formula for the area of a triangle to find the area underneath this curve.
A = 1/2 * bh = 1/2 * (160 ms - 110 ms)(10-3 s / 1 ms)(90 m/s2) = 2.25 m/s
(b) This situation is trickier, because the torso's motion is clearly more complex than the head's. We break this up into segments. Ignore the flat line on the zero axis from 0 ≤ t ≤ 40 ms, because there is no "area" under the function there (and thus it won't contribute to the torso's speed). The segment from 40 ms ≤ t ≤ 100 ms, isolated, forms a triangle, so let's find the area of this part of the acceleration.
AA = 1/2 * (0.0600 s)(50.0 m/s2) = 1.50 m/s
The segment from 100 ms ≤ t ≤ 120 ms is a rectangle, so we can use the area of a rectangle to find the speed here.
AB = ℓw = (0.0200 s)(50.0 m/s2) = 1.00 m/s
The final segment, from 120 ms ≤ t ≤ 160 ms, forms a trapezoid, so we can use the trapezoid formula to find this area.
AC = 1/2 * b(h1 + h2) = 1/2 * (0.0400 s)(50.0 + 20.0) m/s2 = 1.40 m/s
Now add these values together to find the total speed.
v = AA + AB + AC = 1.50 m/s + 1.00 m/s + 1.40 m/s = 3.90 m/s
(a) Focusing on the head's acceleration function, the graph resembles a triangle at t = 160 ms. We use the formula for the area of a triangle to find the area underneath this curve.
A = 1/2 * bh = 1/2 * (160 ms - 110 ms)(10-3 s / 1 ms)(90 m/s2) = 2.25 m/s
(b) This situation is trickier, because the torso's motion is clearly more complex than the head's. We break this up into segments. Ignore the flat line on the zero axis from 0 ≤ t ≤ 40 ms, because there is no "area" under the function there (and thus it won't contribute to the torso's speed). The segment from 40 ms ≤ t ≤ 100 ms, isolated, forms a triangle, so let's find the area of this part of the acceleration.
AA = 1/2 * (0.0600 s)(50.0 m/s2) = 1.50 m/s
The segment from 100 ms ≤ t ≤ 120 ms is a rectangle, so we can use the area of a rectangle to find the speed here.
AB = ℓw = (0.0200 s)(50.0 m/s2) = 1.00 m/s
The final segment, from 120 ms ≤ t ≤ 160 ms, forms a trapezoid, so we can use the trapezoid formula to find this area.
AC = 1/2 * b(h1 + h2) = 1/2 * (0.0400 s)(50.0 + 20.0) m/s2 = 1.40 m/s
Now add these values together to find the total speed.
v = AA + AB + AC = 1.50 m/s + 1.00 m/s + 1.40 m/s = 3.90 m/s
FINAL ANSWERS: (a) 2.25 m/s
(b) 3.90 m/s
(b) 3.90 m/s