•1. A fish maintains its depth in fresh water by adjusting the air content of porous bone or air sacs to make its average density the same as that of the water. Suppose that with its air sacs collapsed, a fish has a density of 1.08 g/cm³. To what fraction of its expanded body volume must the fish inflate the air sacs to reduce its density to that of water?

A: Let's define some variables. If V is the volume of the fish with its air sacs collapsed, and V_a is the volume of the air sacs alone, then the "fraction of its expanded body volume" to which the fish expands its air sacs can be represented by V_a/(V + V_a).

That's what we want to find, but let's set it aside for a moment. All we have that the problem gives us is the density of the fish with its air sacs collapsed, and we want it to be equal to the density of water (the density of water varies slightly depending on the temperature and atmospheric pressure, but in general we can consider it to be 1.00 g/cm³). We might try and set the densities of the water and the fish equal to each other, but this won't help us because our ultimate goal is to find a proportion between the volumes of the fish before and after the expansion, so the method we must use has to consider the variables both when the air sacs are collapsed and when the air sacs are expanded.

The only variable that should be constant before and after the expansion is the mass of the fish, so let's set up a formula in which the fish's mass is considered in both the density of the collapsed fish (ρ_fish) and the density of water (ρ_w):

ρ_fish = m_fish/V

ρ_w = m_fish/(V + V_a)

Since m_fish is the common variable between both densities, we can rewrite these two formulas as one single equation by solving both of them for m_fish and setting them equal to each other:

ρ_fishV = ρ_w(V + V_a)

Now we can use this equation to find the terms we needed in our original expression way back at the beginning of the problem:

(V + V_a)/V = ρ_fish/ρ_w --> V + V_a = (ρ_fish/ρ_w)*V = (1.08 g/cm³/1.00 g/cm³)*V = 1.08V

V + V_a = 1.08V --> V_a = 1.08V - V = 0.08V

Hey look, we now have terms for (V + V_a) and V_a, both of the things we need! Now let's use this to solve for the fraction we set up earlier:

V_a/(V + V_a) = 0.08V/1.08V = 0.074 = 7.4%

FINAL ANSWER: 0.074 / 7.4%

•2. A partially evacuated airtight container has a tight-fitting lid of surface area 77 m² and negligible mass. If the force required to remove the lid is 480 N and the atmospheric pressure is 1.0 x 10⁵ Pa, what is the internal air pressure?

A: A force due to a pressure difference on either side of a surface is represented by F = ΔpA, or F = (p_o - p_i)A, where p_o is the pressure outside the container (the atmospheric pressure), p_i is the pressure inside the container, and A is the area of the lid. We're looking for p_i in this formula, so let's solve:

p_i = p_o - F/A = 1.0 x 10⁵ Pa - (480 N)/(77 m²) = 1.0 x 10⁵ Pa.

FINAL ANSWER: 1.0 x 10⁵ Pa.

•3. Find the pressure increase in the fluid in a syringe when a nurse applies a force of 42 N to the syringe’s circular piston, which has a radius of 1.1 cm.

A: A change in pressure, is represented as Δp = F/A, where F is the applied force and A is the area of the surface to which the force is applied. Because the piston of the syringe is compressing the fluid within the syringe, then the pressure applied to the piston's surface is equal to the pressure increase in the syringe fluids.

The piston is circular, so its surface area is the area of a circle, A = πr². We have the radius of the piston, so let's insert the values into our formula. Keep in mind that the radius is r = 1.1 cm = 0.011 m.

Δp = F/A = F/(πr²) = (42 N)/(π(0.011 m)²) = 1.1 x 10⁵ Pa

FINAL ANSWER: 1.1 x 10⁵ Pa

•4. Three liquids that will not mix are poured into a cylindrical container. The volumes and densities of the liquids are 0.50 L, 2.6 g/cm³; 0.25 L, 1.0 g/cm³; and 0.40 L, 0.80 g/cm³. What is the force on the bottom of the container due to these liquids? One liter = 1 L = 1000 cm³. (Ignore the contribution due to the atmosphere.)

A: The "force on the bottom of the container due to these liquids" will just be the combined weight of the liquids, since those are the only forces acting downwards on the container. Understanding the relationship between density and mass, we can individually calculate the weight of each different liquid. Make sure that the units match up with the units given for the fluids' densities, so convert from liters to cm³ in each case, and use 980 cm/s² for g instead of 9.80 m/s² (I only show the final conversion for W₁, because it's the same for all of them).

W₁ = m₁g = ρ₁V₁g = (2.6 g/cm³)(0.50 L)(1000 cm³/L)(980 cm/s²) = (1.27 x 10⁶ g•cm/s²)(1 kg / 1000 g)(1 m / 100 cm) = 12.7 kg•m/s² = 12.7 N

W₂ = m₂g = ρ₂V₂g = (1.0 g/cm³)(0.25 L)(1000 cm³/L)(980 cm/s²) = 2.5 N

W₃ = m₃g = ρ₃V₃g = (0.80 g/cm³)(0.40 L)(1000 cm³/L)(980 cm/s²) = 3.1 N

The total force on the bottom of the container is the combined weight of all three fluids:

F = W₁ + W₂ + W₃ = 18 N

FINAL ANSWER: 18 N

•5. An office window has dimensions 3.4 m by 2.1 m. As a result of the passage of a storm, the outside air pressure drops to 0.96 atm, but inside the pressure is held at 1.0 atm. What net force pushes out on the window?

A: Because the ambient pressure within the office room has a greater pressure than the atmospheric pressure outside, we have a force due to a pressure difference acting outwards on the window. The formula for a pressure force like this is F = ΔpA, where Δp is the difference in pressure from either side of the surface, and A is the area on which we're focusing - the area of the square window. Let's use our formula, making sure to convert from atm to Pa:

F = ΔpA = (1.0 atm - 0.96 atm)(1.01 x 10⁵ Pa / 1 atm)(3.4 m)(2.1 m) = 2.9 x 10⁴ N

FINAL ANSWER: 2.9 x 10⁴ N

•6. You inflate the front tires on your car to 28 psi. Later, you measure your blood pressure, obtaining a reading of 120/80, the readings being in mm Hg. In metric countries (which is to say, most of the world), these pressures are customarily reported in kilopascals (kPa). In kilopascals, what are (a) your tire pressure and (b) your blood pressure?

A: (a) The conversion rate between psi (or pounds per square inch) and pascals is 1.01 x 10⁵ Pa = 14.7 lb/in². Convert tire pressure:

P = (28 lb/in²)(1.01 x 10⁵ Pa / 14.7 lb/in²)(1 kPa / 1000 Pa) = 190 kPa.

(b) The conversion for mmHg to Pa is 1.01 x 10⁵ Pa = 760 mmHg. Apply this to the blood pressure readings:

(120 mmHg)(1.01 x 10⁵ Pa / 760 mmHg) = 15.9 kPa

(80 mmHg)(1.01 x 10⁵ Pa / 760 mmHg) = 10.6 kPa

FINAL ANSWERS: (a) 190 kPa
(b) 15.9 kPa & 10.6 kPa

••7. In 1654 Otto von Guericke, inventor of the air pump, gave a demonstration before the noblemen of the Holy Roman Empire in which two teams of eight horses could not pull apart two evacuated brass hemispheres. (a) Assuming the hemispheres have (strong) thin walls, so that R in Fig. 14-29 may be considered both the inside and outside radius, show that the force F required to pull apart the hemispheres has magnitude F = πR²Δp, where Δp is the difference between the pressures outside and inside the sphere. (b) Taking R as 30 cm, the inside pressure as 0.10 atm, and the outside pressure as 1.00 atm, find the force magnitude the teams of horses would have had to exert to pull apart the hemispheres. (c) Explain why one team of horses could have proved the point just as well if the hemispheres were attached to a sturdy wall.

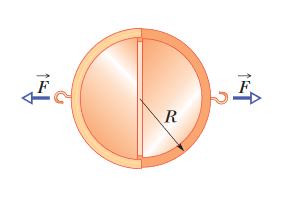
A: The reason why the sphere could not be pulled apart was due to the pressure difference between the inside and outside of the sphere. When the hemispheres were evacuated, the atmospheric pressure was far greater than the sphere's internal pressure, resulting in the incredible force acting on the outside of the sphere. In order for the horses to potentially overcome this force, the team must exert a force at least as great as the horizontal component of the force-due-to-pressure acting on the hemisphere.

(a) So, we want to find the horizontal component of the force due to atmospheric pressure acting on one hemisphere in the direction opposite to the force of the horses. Sort of like this:

For some reason, the official instructor's solutions manual says to do this by setting up a ring-shaped area element around the hemisphere and integrating with respect to the angle from the horizontal. This would certainly work, but it's unnecessarily complicated just as long as you understand that the projected area of a sphere (in other words, the "effective" cross-sectional area from an outside viewpoint) is the same as the area of a two-dimensional circle, πR². Deriving the formula becomes easy:

F = ΔpA_circle = ΔpπR² = πR²Δp

(b) Using the formula we derived above, let's plug in our values, converting everything into SI units:

F = πR²Δp = π(0.30 m)²(1.00 atm - 0.10 atm)(1.01 x 10⁵ Pa / 1 atm) = 2.6 x 10⁴ N

(c) Two teams of horses pulling equal forces in opposite directions would have worked just as well as one team of horse pulling one half of the sphere, while the other half of the sphere was attached to a sturdy wall. This is because of Newton's third law of motion - when the team of horses pulls on the hemisphere away from the wall, this exerts a tension force pulling away from the wall. The wall will, by the third law, exert an equal and opposite force on the hemisphere, pulling the hemisphere toward the wall with a force equal in magnitude and opposite in direction to the force that the horses are exerting. Therefore, using one team of horses and one wall would have been a much more efficient method of performing the experiment.

FINAL ANSWERS: (a) (See derivation above)
(b) 2.6 x 10⁴ N
(c) (See explanation above)

•8. The bends during flight. Anyone who scuba dives is advised not to fly within the next 24 h because the air mixture for diving can introduce nitrogen to the bloodstream. Without allowing the nitrogen to come out of solution slowly, any sudden air-pressure reduction (such as during airplane ascent) can result in the nitrogen forming bubbles in the blood, creating the bends, which can be painful and even fatal. Military special operation forces are especially at risk. What is the change in pressure on such a special-op soldier who must scuba dive at a depth of 20 min seawater one day and parachute at an altitude of 7.6 km the next day? Assume that the average air density within the altitude range is 0.87 kg/m³.

A: The formula for a pressure difference (in a fluid of uniform density) due to a change in height is given by p = ρgh, where "h" is the change in height. Because air and water are both very different fluids, we'll calculate the change in pressure for each height independently.

The gauge pressure at a water depth d of 20 m is p₁ = ρ_seawatergd = (1024 kg/m³)(9.8 m/s²)(20 m) = 2.00 x 10⁵ Pa.

The pressure difference between the soldier standing on the ground and the soldier 7.6 km above is p₂ = ρ_airgh = (0.87 )kg/m³)(9.8 m/s²)(7600 m) = 6.48 x 10⁴ Pa.

These are the two pressure differences in each region (water and air), so the total change in pressure that the soldier will feel should be the sum of these two pressure differences.

Δp = p₁+ p₂ = 2.6 x 10⁵ Pa

FINAL ANSWER: 2.6 x 10⁵ Pa

•9. Blood pressure in Argentinosaurus. (a) If this long-necked, gigantic sauropod had a head height of 21 m and a heart height of 9.0 m, what (hydrostatic) gauge pressure in its blood was required at the heart such that the blood pressure at the brain was 80 torr (just enough to perfuse the brain with blood)? Assume the blood had a density of 1.06 x 10³ kg/m³. (b) What was the blood pressure (in torr or mm Hg) at the feet?

A: (a) We're looking for a gauge pressure, meaning that the ambient atmospheric pressure won't be involved. We just want the pressure due to the presence of the blood. More specifically, we want the pressure due to the difference in height between the heart and the brain, plus the pressure we're supposed to have at the brain. We can use the formula p₂ = p₁ + ρgh, where ρgh is the pressure due to the difference in height, and p₁ is the pressure at the brain, weighing down on the rest of the blood in the body.

p_heart = p_brain + ρgh = 80 torr + (1.06 x 10³ kg/m³)(9.8 m/s²)(21 m - 9.0 m)(1 torr / 1.33.33 Pa) = 1.0 x 10³ torr

(b) At the feet:

p_feet = p_brain + ρgh' = 80 torr + (1.06 x 10³ kg/m³)(9.8 m/s²)(21 m)(1 torr / 133.33 Pa) = 1.7 x 10³ torr

FINAL ANSWERS: (a) 1.0 x 10³ torr
(b) 1.7 x 10³ torr

•10. The plastic tube in Fig. 14-30 has a cross-sectional area of 5.00 cm². The tube is filled with water until the short arm (of length d = 0.800 m) is full. Then the short arm is sealed and more water is gradually poured into the long arm. If the seal will pop off when the force on it exceeds 9.80 N, what total height of water in the long arm will put the seal on the verge of popping?

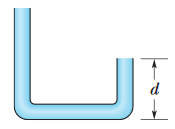
A: The cross-sectional area of the tube is A = 5.00 cm² = 0.000500 m², so we can represent the force acting on the seal as F = pA, where p is the amount of pressure p = ρgh that is set up by the difference in height of the water levels. The total force on the seal is then F = pA = ρghA, and we know that this force must be F = 9.80 N in order for the seal to pop off. Let's rewrite the formula to solve for h:

F = ρghA --> h = F/(ρgA) ≈ 2.0 m

Remember that this only represents the height difference between the y position of the seal and the y position of the water level at the other end of the tube. To find the total height of the water in the long arm, we add this to d, the height of the seal.

d + h = 2.80 m

FINAL ANSWER: 2.80 m

•11. Giraffe bending to drink. In a giraffe with its head 2.0 m above its heart, and its heart 2.0 m above its feet, the (hydrostatic) gauge pressure in the blood at its heart is 250 torr. Assume that the giraffe stands upright and the blood density is 1.06 x 10³ kg/m³. In torr (or mm Hg), find the (gauge) blood pressure (a) at the brain (the pressure is enough to perfuse the brain with blood, to keep the giraffe from fainting) and (b) at the feet (the pressure must be countered by tight-fitting skin acting like a pressure stocking). (c) If the giraffe were to lower its head to drink from a pond without splaying its legs and moving slowly, what would be the increase in the blood pressure in the brain? (Such action would probably be lethal.)

A: (a) Because of gravity, the blood at the brain weighs down on the pressure below it (including at the heart), and thus puts a pressure on the blood where the heart is, so we would typially represent the pressure at the heart as p_heart = p_brain + ρgh. However, since we're looking for the pressure at the brain instead, we rewrite this formula by subtracting ρgh from both sides:

p_brain = p_heart - ρgh = 250 torr - (1.06 x 10³ kg/m³)(9.8 m/s²)(2.0 m)(1 torr / 133.33 Pa) = 94 torr

(b) The gauge pressure at the feet is simpler, since we just apply the same logic used in problem 9.

p_feet = p_heart + ρgh = 250 torr + (1.06 x 10³ kg/m³)(9.8 m/s²)(2.0 m)(1 torr / 133.33 Pa) = 406 torr ≈ 4.1 x 10² torr

(c) Once the giraffe's head has been lowered below its heart, the blood pressure from the heart starts weighing down on and applying additional blood pressure to the head. If the giraffe dips its head down to drink from a pond, then we can imagine that its head will be at feet level, and thus will now be experiencing the same gauge pressure that is felt at the feet. We can find the change in pressure that the head experiences by subtracting the pressure found for the feet from the pressure found at the brain.

Δp = p_feet - p_brain = 406 torr - 94 torr = 312 torr ≈ 3.1 x 10² torr

FINAL ANSWERS: (a) 94 torr
(b) 4.1 x 10² torr
(c) 3.1 x 10² torr

•12. The maximum depth d_max that a diver can snorkel is set by the density of the water and the fact that human lungs can function against a maximum pressure difference (between inside and outside the chest cavity) of 0.050 atm. What is the difference in d_max for fresh water and the water of the Dead Sea (the saltiest natural water in the world, with a density of 1.5 x 10³ kg/m³)?

A: If the hydrostatic pressure acting on a person at a depth is p = ρ_liquidgd, then the depth for a maximum pressure difference of 0.050 atm is

d_max = p/(ρ_liquidg) = (0.050 atm)/(ρ_liquidg) = (5065 Pa)/(ρ_liquidg)

Of course, we want the difference in this "max depth" value between fresh water (ρ_fw = 998 kg/m³) and Dead Sea water (ρ_sw = 1500 kg/m³). Let's subtract these values.

Δd_max = (5065 Pa)/(ρ_fwg) - (5065 Pa)/(ρ_swg) = (5065 Pa)/g * (1/ρ_fw - 1/ρ_sw) = (5065 Pa)/(9.8 m/s²) * [1/(998 kg/m³) - 1/(1500 kg/m³)] = 0.17 m

FINAL ANSWER: 0.17 m

•13. At a depth of 10.9 km, the Challenger Deep in the Marianas Trench of the Pacific Ocean is the deepest site in any ocean. Yet, in 1960, Donald Walsh and Jacques Piccard reached the Challenger Deep in the bathyscaph Trieste. Assuming that seawater has a uniform density of 1024 kg/m³, approximate the hydrostatic pressure (in atmospheres) that the Trieste had to withstand. (Even a slight defect in the Trieste structure would have been disastrous.)

A: We're looking for the hydrostatic pressure (meaning, the pressure solely due to the water) acting on the bathyscaph, so we disregard atmospheric pressure and look for the gauge pressure due to the bathyscaph's depth in the water.

p = ρgh = (1024 kg/m³)(9.8 m/s²)(10.9 x 10³ m)(1 atm / 1.01 x 10⁵ Pa) ≈ 1.08 x 10³ atm

FINAL ANSWER: 1.08 x 10³ atm

•14. Calculate the hydrostatic difference in blood pressure between the brain and the foot in a person of height 1.83 m. The density of blood is 1.06 x 10³ kg/m³.

A: We're asked to find the pressure difference, not the gauge pressure, so we can ignore the pressure in the person's brain and just use our formula for the pressure difference due to a height difference:

Δp = ρgh = (1.06 x 10³ kg/m³)(9.8 m/s²)(1.83 m) = 1.90 x 10⁴ Pa

FINAL ANSWER: 1.90 x 10⁴ Pa

•15. What gauge pressure must a machine produce in order to suck mud of density 1800 kg/m³ up a tube by a height of 1.5 m?

A: "Sucking" occurs when there's a difference in pressure between the atmospheric pressure and the pressure within the machine. We will just use the typical gauge pressure formula here, except our value for pressure here will be negative - gauge pressure is negative when the absolute pressure is less than the atmospheric pressure. This is also consistent with the derivation of the gauge pressure formula as well, because the "h" variable originally represented a "depth" value, where the pressure difference is due to some pressure acting above the point. Since mud is being pushed upwards through the tube against gravity, it makes sense that the value should be negative.

p_g = ρg(-h) = -(1800 kg/m³)(9.8 m/s²)(1.5 m) = -2.6 x 10⁴ Pa

FINAL ANSWER: -2.6 x 10⁴ Pa

•16. Snorkeling by humans and elephants. When a person snorkels, the lungs are connected directly to the atmosphere through the snorkel tube and thus are at atmospheric pressure. In atmospheres, what is the difference Δp between this internal air pressure and the water pressure against the body if the length of the snorkel tube is (a) 20 cm (standard situation) and (b) 4.0 m (probably lethal situation)? In the latter, the pressure difference causes blood vessels on the walls of the lungs to rupture, releasing blood into the lungs. As depicted in Fig. 14-31, an elephant can safely snorkel through its trunk while swimming with its lungs 4.0 m below the water surface because the membrane around its lungs contains connective tissue that holds and protects the blood vessels, preventing rupturing.

A: If a person's lungs are connected to the air through a snorkel tube, they have the atmospheric pressure within their lungs, and some amount of pressure is acting onto the lungs due to the hydrostatic pressure when the person is at some depth. The pressure difference in both cases, then, is equal to the gauge pressure at those depths in the water.

(a) Δp = ρgh = (998 ³ kg/m³)(9.8 m/s²)(0.20 m)(1 atm / 1.01 x 10⁵ Pa) = 0.019 atm

(b) Δp = ρgh = (998 ³ kg/m³)(9.8 m/s²)(4.0 m)(1 atm / 1.01 x 10⁵ Pa) ≈ 0.39 atm

FINAL ANSWERS: (a) 0.019 atm
(b) 0.39 atm

•17. Crew members attempt to escape from a damaged submarine 100 m below the surface. What force must be applied to a pop-out hatch, which is 1.2 m by 0.60 m, to push it out at that depth? Assume that the density of the ocean water is 1024 kg/m³ and the internal air pressure is at 1.00 atm.

A: The force that needs to be applied to the hatch is due to the pressure difference between the inside and the outside of the submarine. Outside the submarine, the pressure acting on the submarine is p₀ + ρgd, where p₀ is the atmospheric pressure, 1.00 atm. We find the pressure difference:

1.00 atm + ρgd - 1.00 atm = ρgd

The net pressure acting on the submarine is ρgd. We're looking for the amount of force that we require to open the door, so we use the formula for the force due to a pressure.

F = pA = (ρgd)A = (1024 kg/m³)(9.8 m/s²)(100 m)(1.2 m)(0.60 m) = 7.2 x 10⁵ N

FINAL ANSWER: 7.2 x 10⁵ N

•18. In Fig. 14-32, an open tube of length L = 1.8 m and cross-sectional area A = 4.6 cm² is fixed to the top of a cylindrical barrel of diameter D = 1.2 m and height H = 1.8 m. The barrel and tube are filled with water (to the top of the tube). Calculate the ratio of the hydrostatic force on the bottom of the barrel to the gravitational force on the water contained in the barrel. Why is that ratio not equal to 1.0? (You need not consider the atmospheric pressure.)

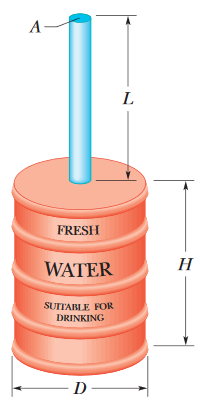
A: Let's use what we know about pressure and forces to find the force due to hydrostatic pressure at the bottom of the barrel, and the force due to gravity acting on the water in the barrel.

F_h = p_hA = ρg(L + H)A

F_g = mg = ρVg = ρAHg

Now we take the ratio of F_h to F_g.

F_h/F_g = (ρg(L + H)A)/(ρAHg) = (L + H)/H

Since L = H in this case, the ratio is 2.0.

The ratio will only be equal to 1.0 if both forces are equal. The forces should not be equal in this case - the force due to gravity used here only considers the water in the lower barrel, while the hydrostatic gauge pressure considers the presence of the water in the upper tube as well. This additional pressure causes the force to be greater.

FINAL ANSWER: 2.0 - See explanation above.

••23. In analyzing certain geological features, it is often appropriate to assume that the pressure at some horizontal level of compensation, deep inside Earth, is the same over a large region and is equal to the pressure due to the gravitational force on the overlying material. Thus, the pressure on the level of compensation is given by the fluid pressure formula. This model requires, for one thing, that mountains have roots of continental rock extending into the denser mantle (Fig. 14-34). Consider a mountain of height H = 6.0 km on a continent of thickness T = 32 km. The continental rock has a density of 2.9 g/cm³, and beneath this rock the mantle has a density of 3.3 g /cm³. Calculate the depth D of the root. (Hint: Set the pressure at points a and b equal; the depth y of the level of compensation will cancel out.)

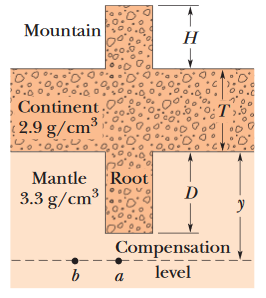
A: Since the pressure should be equal at both points a and b (going off of this "compensation level" premise), we should be able to take the gauge pressures at both points as though they were equal. As such, let's set both pressures equal to one another, with careful regard for the fact that different materials of different densities are acting above both points.

Let ρ_c be the density of the continental crust material, and ρ_m be the density of the mantle material.

p_a = p_b

ρ_cg(H + T + D) + ρ_mg(y - D) = ρ_cgT + ρ_mgy

We want to solve for D.

ρ_c(H + T + D) + ρ_m(y - D) = ρ_cT + ρ_my

ρ_cH + ρ_cT + ρ_cD + ρ_my - ρ_mD = ρ_cT + ρ_my

ρ_cH + ρ_cD - ρ_mD = 0

ρ_cH = ρ_mD - ρ_cD

ρ_cH = D(ρ_m - ρ_c)

--> D = ρ_cH/(ρ_m - ρ_c) = (6.0 km)(2.9 g/cm³)/(3.3 g /cm³ - 2.9 g/cm³) = 44 km

FINAL ANSWER: 44 km

•••24. In Fig. 14-35, water stands at depth D = 35.0 m behind the vertical upstream face of a dam of width W = 314 m. Find (a) the net horizontal force on the dam from the gauge pressure of the water and (b) the net torque due to that force about a horizontal line through O parallel to the (long) width of the dam. This torque tends to rotate the dam around that line, which would cause the dam to fail. (c) Find the moment arm of the torque.

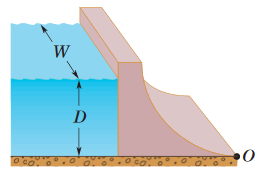
A: (a) Since pressure (in all directions) increases with depth within a fluid, the pressure acting on the wall of the damn from the reservoir is not uniform. Therefore, the force acting on the wall isn't uniform either. We can find the total force on the wall by taking a horizontal strip of a differential area, dA, and integrate along the vertical axis of the wall. Let's say that this strip has the same width as the width of the reservoir, W, and it has a thickness of dy. We will also use the variable "y" to represent the depth of this strip element at any given point, since the gauge pressure at any depth in water is a function of the depth. The force element at any depth of the wall is then:

dF = p(dA) = (ρgy)(Wdy) = ρgyWdy

Now we integrate this along the height of D, the total depth of the water in the reservoir. We integrate from a depth of 0 meters, all the way down to the deepest point in the water (represented by D).

F = ∫₀^DρgyWdy = ρgW∫₀^Dydy

Based on the power rule of integration, the indefinite integral of this (ignoring the "outside" constants) is 1/2 * y² + C. We now apply the fundamental theorem of calculus.

1/2 * ρgWy²|_{y = 0}^{y = D} = [1/2 * ρgWD²] - [1/2 * ρgW(0)²] = 1/2 * ρgWD²

Now we plug in our values.

F = 1/2 * ρgWD² = 1/2 * (1.00 x 10³ kg/m³)(9.80 m/s²)(314 m)(35.0 m)² = 1.88 x 10⁹ N

This is part of the reason why dams are usually sloped or slanted this way; as the pressure becomes greater with water depth, the damn must be stronger in order to resist the greater pressure force at the lower levels.

(b) Because torque is a type of force, it seems intuitive that the torque being applied to the wall of the dam by the water won't be uniform either, so we'll have to perform an integration again. It could be confusing to work with the complex shape of this dam, especially since we're not given any information about the dam's geometry, so let's simplify the dam as though it were a single rod on which the water is acting. It might seem strange that we're changing the geometry of the dam so much, but this actually won't change our answer at all; No matter what the dam looks like, the water is still only directly acting on the wall where the water and the dam make contact. Yes, the position and angle of the moment arm changes, but we're still only looking at the horizontal components of that arm. This is another part of the reason why dams are often shaped this way; since the dam's engineers can't change the torque that the water exerts on the dam, they instead increase the torque due to the gravitational force acting on the dam by putting its center of mass further away from where the axis of rotation is. This gravitational torque counters the torque due to the water. But I digress...

Anyway, the torque (or in this case, the torque element, since we know we'll be integrating) acting on this dam is equal to the product of the force element, dF, and the lever arm, which changes with depth. I will call it (D - y), since the torque will equal to zero at the lowest depth where the axis of rotation is, and maximized when the depth is zero. We expand this using what we know about dF from part (a):

dτ = dF(D - y) = ρgyW(D - y)dy

Now we integrate from 0 to D, over the depth of the water again.

τ = ∫₀^DρgyW(D - y)dy = ρgW∫₀^Dy(D - y)dy = ρgW∫₀^DDy - y²dy

= ρgW(1/2 * Dy² - 1/3 * y³)|_{y = 0}^{y = D} = [ρgW(1/2 * D³ - 1/3 * D³)] - [ρgW(1/2 * (0)³ - 1/3 * (0)³)] = ρgW(1/2 * D³ - 1/3 * D³)

= 1/6 * ρgWD³

Now we plug in the values given by the problem.

τ = 1/6 * ρgWD³ = 1/6 * (1.00 x 10³ kg/m³)(9.80 m/s²)(314 m)(35.0 m)³ = 2.20 x 10¹⁰ N•m

(c) We can find the length of the lever arm "r" by recalling that the formula for a torque is defined as τ = rF, where r and F are perpendicular to each other (which they are in this case). We spent the previous two parts of the problem solving for τ and F, so now all we need to do is solve for r.

r = τ/F = [1/6 * ρgWD³]/[1/2 * ρgWD²] = D/3 = (35.0 m)/3 = 11.7 m

This means that the effective line of action of the total force exerted by the water is at a distance D/3 above the bottom level of the dam.

FINAL ANSWERS: (a) 1.88 x 10⁹ N
(b) 2.20 x 10¹⁰ N•m
(c) 11.7 m

•25. In one observation, the column in a mercury barometer (as is shown in Fig. 14-5a) has a measured height h of 740.35 mm. The temperature is -5.0° C, at which temperature the density of mercury ρ is 1.3608 x 10⁴ kg/m³. The free-fall acceleration g at the site of the barometer is 9.7835 m/s². What is the atmospheric pressure at that site in pascals and in torr (which is the common unit for barometer readings)?

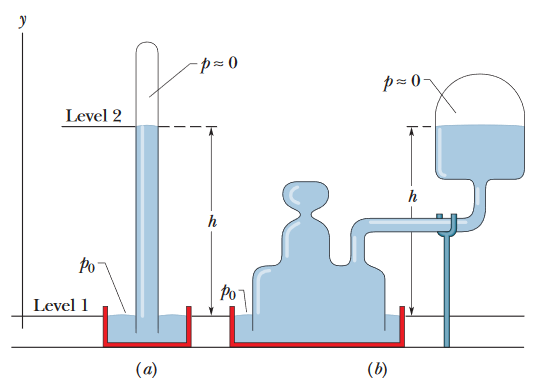
A: We use the formula for atmospheric pressure based on a mercury barometer reading.

p₀ = ρgh = (1.3608 x 10⁴ kg/m³)(9.7835 m/s²)(.74035 m)(1 torr / 133.33 Pa) = 739.26 torr

FINAL ANSWER: 739.26 torr

•26. To suck lemonade of density kg/m³ up a straw to a maximum height of 4.0 cm, what minimum gauge pressure (in atmospheres) must you produce in your lungs?

A: We are measuring the gauge pressure within the lungs. If we think of the lung as a closed "vessel", and the straw as an open tube, then this lung-straw system is similar to that of an open-tube manometer. We use the formula for the internal gauge pressure that a manometer uses (and keep in mind the fact that it must be negative, since the pressure inside your lung is less than the outside atmospheric pressure).

p = -ρgh = -(1000 kg/m³)(9.8 m/s²)(4.0 x 10^-2 m)(1 atm / 1.01 x 10⁵ Pa) = -3.9 x 10^-3 atm

FINAL ANSWER: -3.9 x 10^-3 atm

•28. A piston of cross-sectional area a is used in a hydraulic press to exert a small force of magnitude f on the enclosed liquid. A connecting pipe leads to a larger piston of cross-sectional area A (Fig. 14-36). (a) What force magnitude F will the larger piston sustain without moving? (b) If the piston diameters are 3.80 cm and 53.0 cm, what force magnitude on the small piston will balance a 20.0 kN force on the large piston?

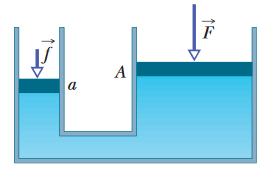
A: For the forces to balance, F and f must be equal. According to Pascal's Principle, a change in pressure in an incompressible fluid is equal throughout the hydraulic lever. Therefore,

F/A = f/a --> F = (A/a)f.

This will tell us the force we need on the smaller piston to balance out any force from the larger one.

(b) F/A = f/a --> f = (a/A)F = [(3.80 cm)²/(53.0 cm)²]*(20.0 x 10³ N) = 103 N

FINAL ANSWERS: (a) F = (A/a)f.
(b) 103 N

•30. A 5.00 kg object is released from rest while fully submerged in a liquid. The liquid displaced by the submerged object has a mass of 3.00 kg. How far and in what direction does the object move in 0.200 s, assuming that it moves freely and that the drag force on it from the liquid is negligible?